SAT Math: Practice Questions-Additional topics in math-Angles, arc lengths, and trig functions

SAT MathsSAT EnglishSAT Practice Tests -(Full -Length)

SAT Math Practice Questions-All Topics

Question

                   In the figure shown, C is the center of the circle and \(\overline{AB}\) is tangent to the circle at A. Which of the following is true about the measure of angle BAC? 

  1. The measure is less than 90°
  2. The measure is greater than 90°
  3. The measure is equal to 90°
  4. It cannot be determined whether the measure is less than, greater than, or equal to 90°
Answer/Explanation

Ans: C

Question

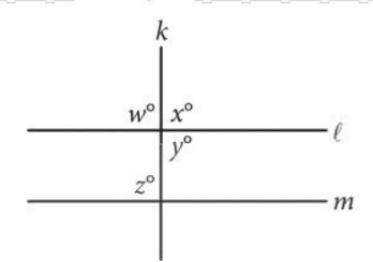
In the figure, lines \(l\) and \(m\) each intersect line \(k\). Which of the following is sufficient to prove that lines \(l\) and \(m\) are parallel?

  1. \(w\)=\(y\)
  2. \(w\)=\(z\)
  3. \(x\)=\(y\)
  4. \(x\)=\(z\)
Answer/Explanation

Ans: B

Question

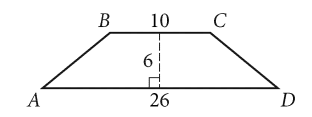
In the figure shown, \overline{BC} is parallel to \overline{AD} and AB=CD. What is the perimeter of quadrilateral ABCD?

Answer/Explanation

Ans: 56

Question


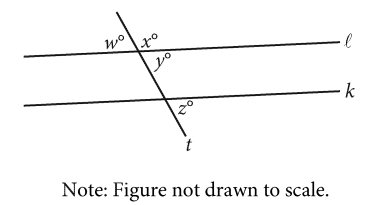
In the figure shown, line \(t\) intersects lines \(l\) and \(k\). Which additional piece of information is sufficient to prove that lines \(l\) and \(k\) are parallel? 

  1. \(x\) > 90
  2. \(w\) < 90
  3. \(w\) = \(y\)
  4. \(y\) = \(z\)
Answer/Explanation

Ans: D

Question

Rectangle A has an area of 64 square meters. The length and width of rectangle B are 3 times the corresponding length and width of rectangle A. What is the area, in square meters, of rectangle B? 

Answer/Explanation

Ans: 576

Question

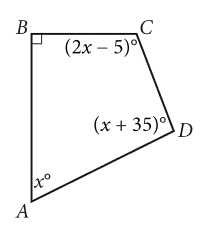
Quadrilateral ABCD is shown. Which equation shows how the measures of the angles of the quadrilateral are related?

  1. \(x + 90 + (2x – 5) + (x + 35) = 360\)
  2. \(4(x+90+(2x-5)+(x+35))=360 \)
  3. \(x + (2x – 5) + (x + 35) = 360\)
  4. \(4(x+(2x-5)+(x+35))=360\)
Answer/Explanation

Ans: A

Question

The side length of square \(ABCD\) is twice the side length of square \(EFGH\). If the area of square \(EFGH\) is 9, what is the area of square \(ABCD\) ? 

Answer/Explanation

Ans: 36

More SAT Math Practice Questions.............
Scroll to Top