Digital SAT Math: Linear equations in two variables -Practice Questions - New Syllabus
DSAT MAth Practice questions – all topics
- Algebra Weightage: 35% Questions: 13-15
- Linear equations in one variable
- Linear equations in two variables
- Linear functions
- Systems of two linear equations in two variables
- Linear inequalities in one or two variables
DSAT MAth and English – full syllabus practice tests
Question Easy
A line in the \(x y\)-plane passes through the point \((0,5)\) and has a slope of 7 . What is an equation of this line?
A) \(y=5 x-7\)
B) \(y=5 x+7\)
C) \(y=7 x-5\)
D) \(y=7 x+5\)
▶️Answer/Explanation
Answer:D
The equation of a line in slope-intercept form is given by:
\(
y = mx + b
\)
where \(m\) is the slope and \(b\) is the \(y\)-intercept.
Given:
Slope (\(m\)) = 7
Point \((0, 5)\) indicates that the \(y\)-intercept (\(b\)) is 5.
Substituting these values into the slope-intercept form:
\(
y = 7x + 5
\)
Question Easy
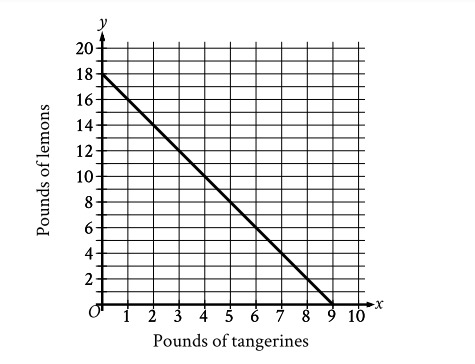
The graph shows the possible combinations of the number of pounds of tangerines and lemons that could be purchased for \(\$ 18\) at a certain store. If Melvin purchased lemons and 4 pounds of tangerines for a total of \(\$ 18\), how many pounds of lemons did he purchase?
A.7
B.10
C.14
D.16
▶️Answer/Explanation
Answer: B
Locate the given $x$-value on the graph.
We are given that Melvin bought 4 pounds of tangerines (\( x = 4 \)).
Find \( x = 4 \) on the \(x\)-axis.
Find the corresponding \(y\)-value
Move vertically from \( x = 4 \) until you hit the line.
Read the corresponding \( y \)-value on the $y$-axis.
From the graph, when \( x = 4 \), the corresponding \( y \)-value is \(10\).
So, Melvin purchased \(10\) pounds of lemons.
Question Easy
\(4x+3y=24\)
Mario purchased 4 binders that cost x dollars each and 3 notebooks that cost y dollars each. If the given equation represents this situation, which of the following is the best interpretation of 24 in this context?
A. The total cost, in dollars, for all binders purchased
B. The total cost, in dollars, for all notebooks purchased
C. The total cost, in dollars, for all binders and notebooks purchased
D. The difference in the total cost, in dollars, between the number of binders and notebooks purchased
▶️Answer/Explanation
Answer: C
\(
4x + 3y = 24
\)
4x → Total cost of 4 binders
3y → Total cost of 3 notebooks
24 → Represents the total cost of binders and notebooks.
Question Easy
Line \(l\) has a slope of -3 and an \(x\)-intercept of \(\left(\frac{9}{2}, 0\right)\). What is the \(y\)-intercept of line \(l\) ?
A) \(\left(\frac{9}{2}, 0\right)\)
B) \(\left(0, \frac{9}{2}\right)\)
C) \(\left(\frac{27}{2}, 0\right)\)
D) \(\left(0, \frac{27}{2}\right)\)
▶️Answer/Explanation with Desmos
Answer: D
Question Easy
A certain university offers courses that are either 3 credits or 4 credits per course each semester. A student registered for a total of 16 credits for the fall semester. Which equation represents the possible number of 3-credit courses, $x$, and 4-credit courses, $y$, that the student could have registered for?
A) $3 x+4 y=7$
B) $3 x+4 y=16$
C) $x+y=7$
D) $x+y=16$
▶️Answer/Explanation
Answer: B
Each 3-credit course contributes \( 3x \) credits, and each 4-credit course contributes \( 4y \) credits. The total number of credits is 16.
Thus, the equation is:
\(3x + 4y = 16\)
