Question
Which of the following is equivalent to \(4x^3+8x^2\)
- \(12x^5\)
- \(12x^2(2x+1)\)
- \(4x^2(x+2)\)
- \(x^2(12+x)\)
Answer/Explanation
Ans: C
Question
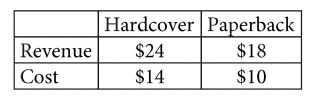
A certain book is available from a publishing company in both hardcover and paperback. The table shows the revenue and cost in 2016 for each of the hardcover and paperback books produced by the company.
In 2016 the total cost for 200 of the books that were sold was between \($\)2,200 and \($\)2,400. Which of the following could be the number of hardcover books that were sold?
- 80
- 120
- 160
- 200
Answer/Explanation
Ans: A
Question

A certain book is available from a publishing company in both hardcover and paperback. The table shows the revenue and cost in 2016 for each of the hardcover and paperback books produced by the company.
An analyst estimates that the cost of each of the paperback books will increase \($\)0.50 each year after 2016. Which of the following models the cost \(c\), in dollars, of each of the paperback books \(t\) years after 2016?
- \(c = 0.5 + 10t\)
- \(c= 0.5+18t\)
- \(c= 10+0.5t\)
- \(c= 18+0.5t\)
Answer/Explanation
Ans: C
Question
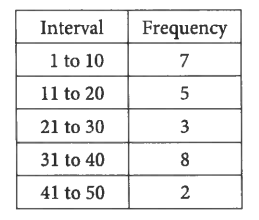
Each of the 25 data values in a data set is a different integer between 1 and 50, inclusive. The table gives the frequency of the data for five intervals. Which of the following intervals contains exactly \(\frac{2}{5}\) of the values in the data set?
- 1 to 20
- 11 to 30
- 21 to 40
- 31 to 50
Answer/Explanation
Ans: D
Question
The line graph shows the total length, in miles, of major commercial railroad tracks in the United States from 1916 to 1976.
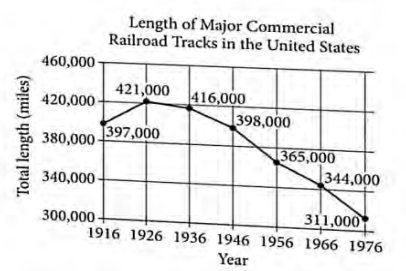
The average rate of change, in miles per year, of the total length of major commercial railroad tracks in the United States from 1916 to 1926 is \(m\). What is the value of \(m\)?
Answer/Explanation
Ans: 2400
Question
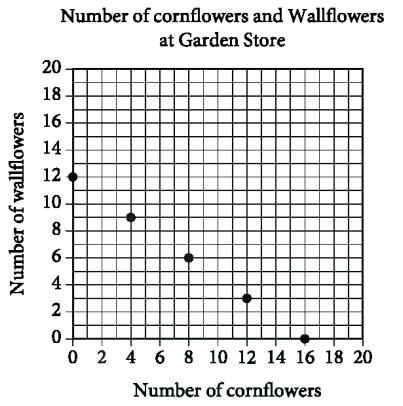
The points plotted in the coordinate plane above represent the possible numbers of wallflowers and cornflowers that someone can buy at the Garden the Store in order to spend exactly \($\)24.00 total on the two types of flowers. The price of each wallflower is the same and the price of each cornflower is the same. What is the price, in dollars, of 1 cornflower? (Disregard the \($\) sign when gridding your answer. For example, if your answer is \($\)9.87, grid 9.87)
Answer/Explanation
Ans: 3/2, 1.5
Question
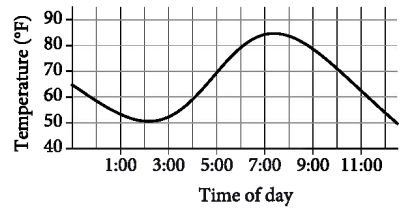
The graph above shows the temperature in a room during a day when the thermostat malfunctioned. For which of the following two-hour periods was difference between the maximum and minimum temperatures greatest?
- 1:00 to 3:00
- 3:00 to 5:00
- 5:00 to 7:00
- 7:00 to 9:00
Answer/Explanation
Ans: B
