SAT Math: Practice Questions-Problem solving and data analysis- Scatterplots

SAT MathsSAT EnglishSAT Practice Tests -(Full -Length)

SAT Math Practice Questions-All Topics

Question

For a particular cross-country skier, each point in the scatterplot gives the skier’s heart rate, in beats per minute (bpm), and the skier’s oxygen uptake, in liters per minute (L/min), as measured at various points on a cross-country ski course. A line of best fit is also shown.

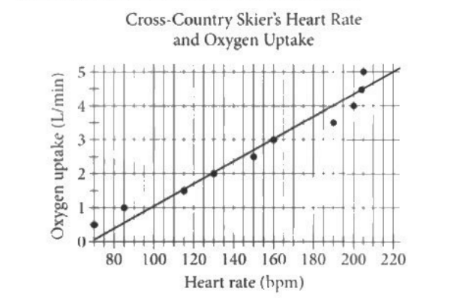
When the skier’s heart rate was 85 bpm, which of the following is closest to the difference, in L/min, between the skier’s actual oxygen uptake and the oxygen uptake predicted by the line of best fit shown? 

  1. 0.5
  2. 1.0
  3. 2.5
  4. 5.0
Answer/Explanation

Ans: A

Question

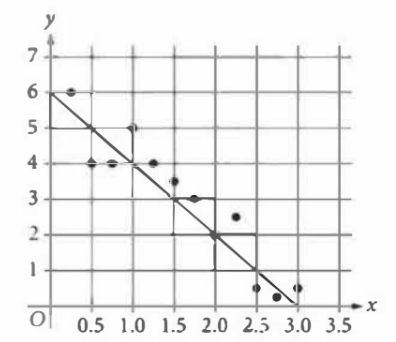
The scatterplot shows 12 values from a data set. A line of best fit for the data is also shown. Which of the following is the best interpretation of the \(y\)-coordinate of the \(y\)-intercept of the line of best fit?

  1. For the value \(x\) =6, the line of best fit predicts the corresponding \(y\)-value to be approximately 0.
  2. For the value \(y\) =0, the line of best fit predicts the corresponding \(x\)-value to be approximately 3.
  3. For the value \(x\) = 0 , the line of best fit predicts the corresponding \(y\)-value to be approximately 6.
  4. For the value \(y\) = 3 , the line of best fit predicts the corresponding \(x\)-value to be approximately 0.
Answer/Explanation

Ans: C

Question

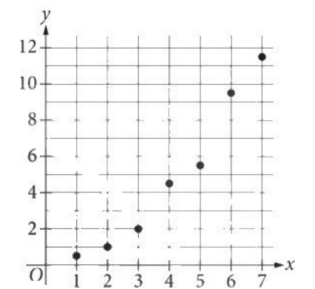
Which equation is the most appropriate quadratic model for the data shown in the scatterplot?

  1. \(y\)=4\(x\)2
  2. \(y\)=2\(x\)2
  3. \(y\)=(1/2)\(x\)2
  4. \(y\)=(1/4)\(x\)2
Answer/Explanation

Ans: D

Question

The scatterplot shows the relationship between two variables, \(x\) and \(y\). A line of best fit is also shown.

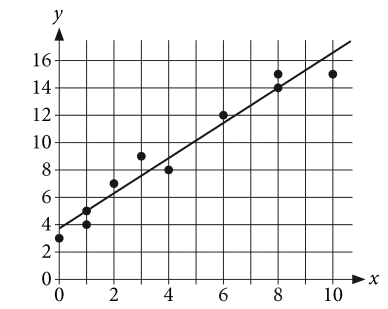
What is an equation of the line of best fit?

  1. \(y\)=3.7+1.3\(x\)
  2. \(y\)=1.3+3.7\(x\)
  3. \(y\)=3.7-1.3\(x\)
  4. \(y\)=1.3-3.7\(x\)
Answer/Explanation

Ans: A

Question

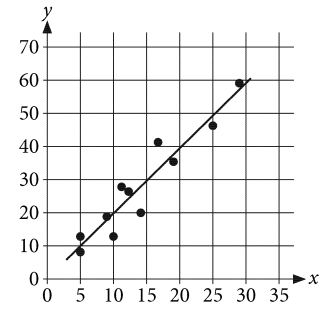
The scatterplot shows a data set of 11 points and a line of best fit for the data. For how many data points is the \(y\)-value predicted by the line of best fit greater than the actual \(y\)-value?

  1. Five
  2. Six
  3. Seven
  4. Eight
Answer/Explanation

Ans: A

Question

.

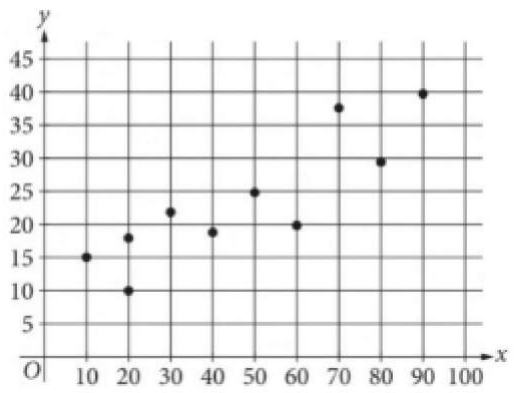
The scatterplot shows 10 values from a data set. Which of the following equations is the most appropriate linear model for the data shown?

  1. \(y=9+\frac{3}{10}x\)
  2. \(y=9-\frac{3}{10}x\)
  3. \(y=\frac{6}{5}x\)
  4. \(y=\frac{3}{8}x\)
Answer/Explanation

Ans: A

 

Question

The scatterplot shows the average price per square foot of a house in the United States each year for several years. A line of best fit for the data is also shown.

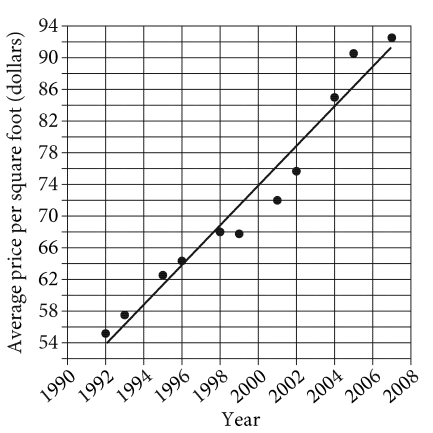
The line of best fit predicted that the average price per square foot in 2001 would be \($\)76. What is the difference between the predicted value and the actual average price per square foot in 2001? 

  1. \($\)0
  2. \($\)2
  3. \($\)4
  4. \($\)6
Answer/Explanation

Ans: C

More SAT Math Practice Questions.............
Scroll to Top