6.1 Circular motion
Essential Idea:
A force applied perpendicular to its displacement can result in circular motion.
Understandings:
- Period, frequency, angular displacement and angular velocity
- Centripetal force
- Centripetal acceleration
Applications and Skills:
- Identifying the forces providing the centripetal forces such as tension, friction, gravitational, electrical, or magnetic
- Solving problems involving centripetal force, centripetal acceleration, period, frequency, angular displacement, linear speed and angular velocity
- Qualitatively and quantitatively describing examples of circular motion including cases of vertical and horizontal circular motion
Data booklet reference:
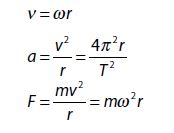
UNIFORM AND NON-UNIFORM CIRCULAR MOTION
UNIFORM CIRCULAR MOTION
An object moving in a circle with a constant speed is said to be in uniform circular motion. Example – Motion of the tip of the second hand of a clock.
ANGULAR DISPLACEMENT : Change in angular position is called angular displacement (dθ).
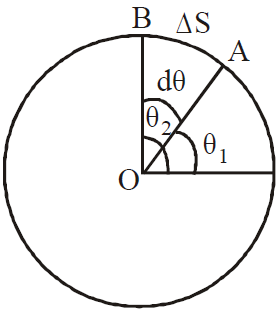
ANGULAR VELOCITY : Rate of change of angular displacement is called angular velocity ω
i.e.,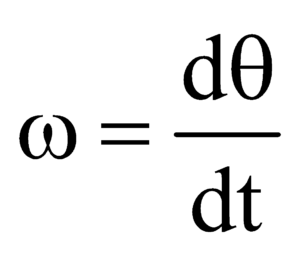 
Relation between linear velocity (v) and angular velocity (ω).
ANGULAR ACCELERATION : Rate of change of angular velocity is called angular acceleration.
i.e.,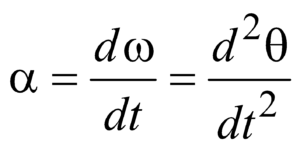 
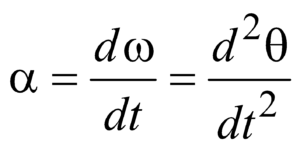
Relation between linear acceleration and angular acceleration.
CENTRIPETAL ACCELERATION : Acceleration acting on a body moving in uniform circular motion is called centripetal acceleration. It arises due to the change in the direction of the velocity vector.
Magnitude of centripetal acceleration is
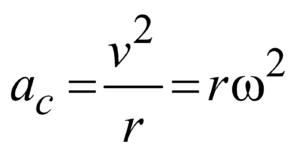
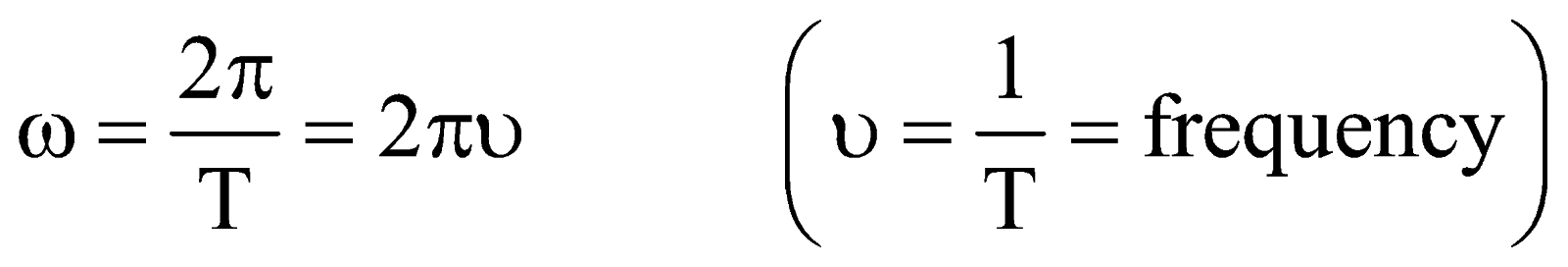
This acceleration is always directed radially towards the centre of the circle.
CENTRIPETAL FORCE : The force required to keep a body moving in uniform circular motion is called centripetal force.
It is always directed radially inwards.
CENTRIFUGAL FORCE : Centrifugal force is a fictitious force which acts on a body in rotating (non-inertial frames) frame of reference.
Magnitude of the centrifugal force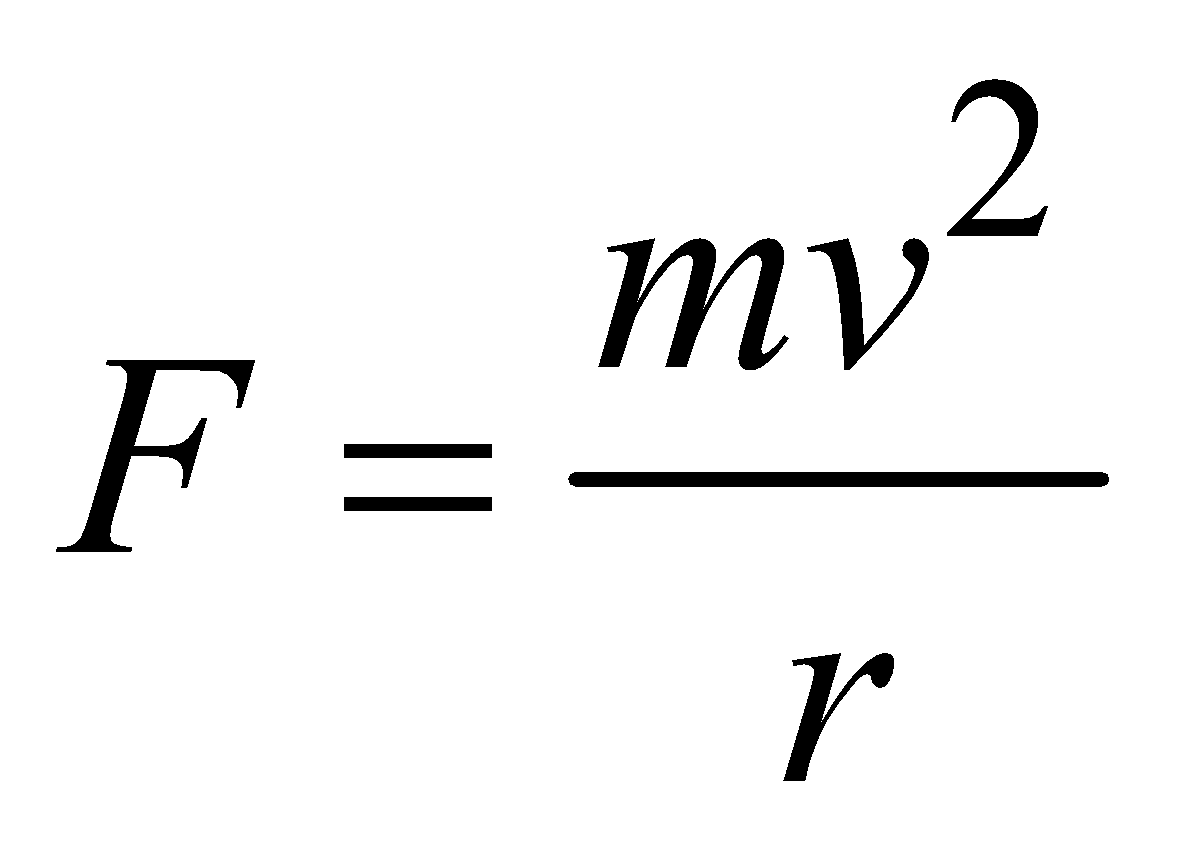 
This force is always directed radially outwards and is also called coriolis force.
NON-UNIFORM CIRCULAR MOTION
An object moving in a circle with variable speed is said to be in non-uniform circular motion.
If the angular velocity varies with time, the object has two accelerations possessed by it, centripetal acceleration (ac) and Tangential acceleration (aT) and both perpendicular to each other.
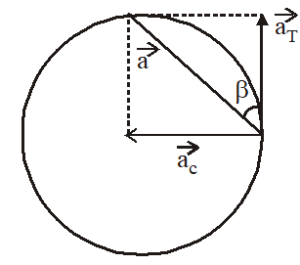
Net acceleration
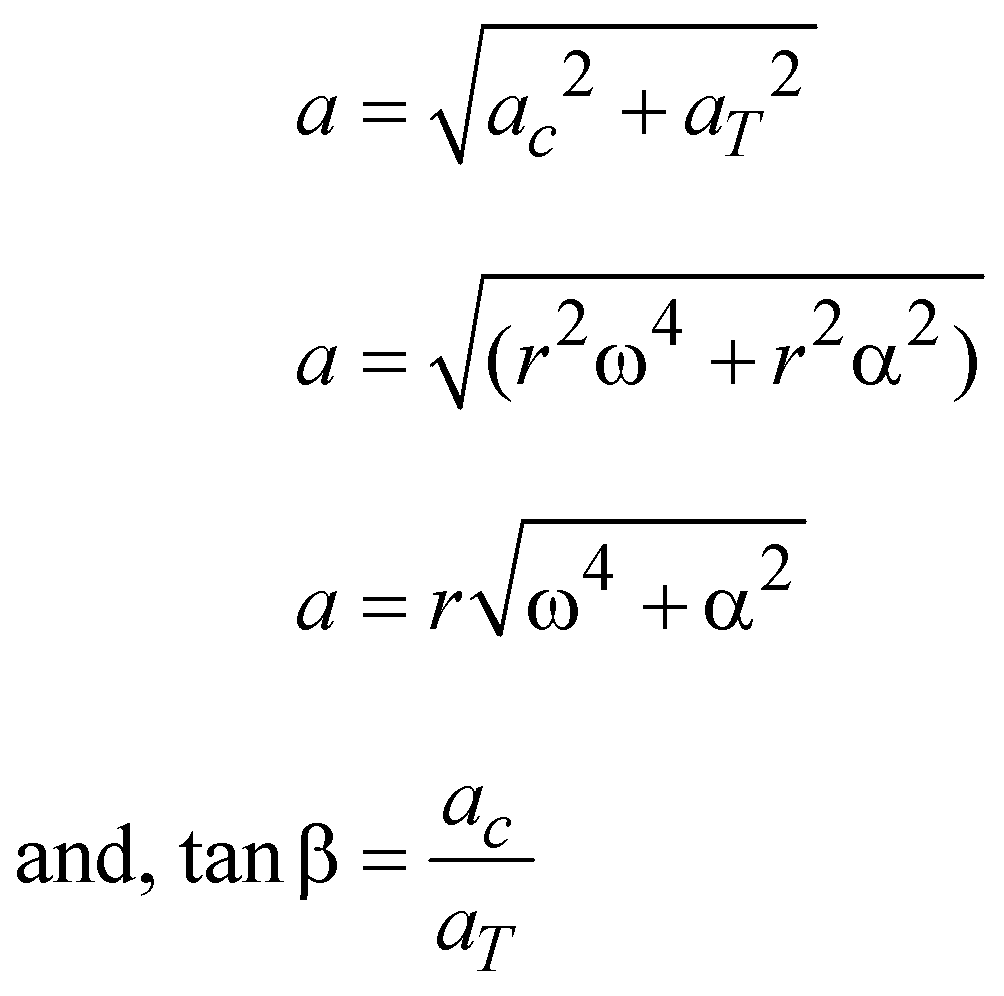
KEEP IN MEMORY
- Angular displacement behaves like vector, when its magnitude is very small. It follows laws of vector addition.
- Angular velocity and angular acceleration are axial vectors.
- Centripetal acceleration always directed towards the centre of the circular path and is always perpendicular to the instantaneous velocity of the particle.
- Circular motion is uniform if aT = rα = 0, that is angular velocity remains constant and radial acceleration
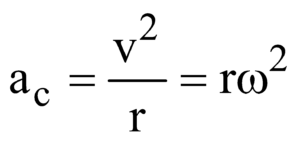is constant. - When aT or α is present, angular velocity varies with time and net acceleration is
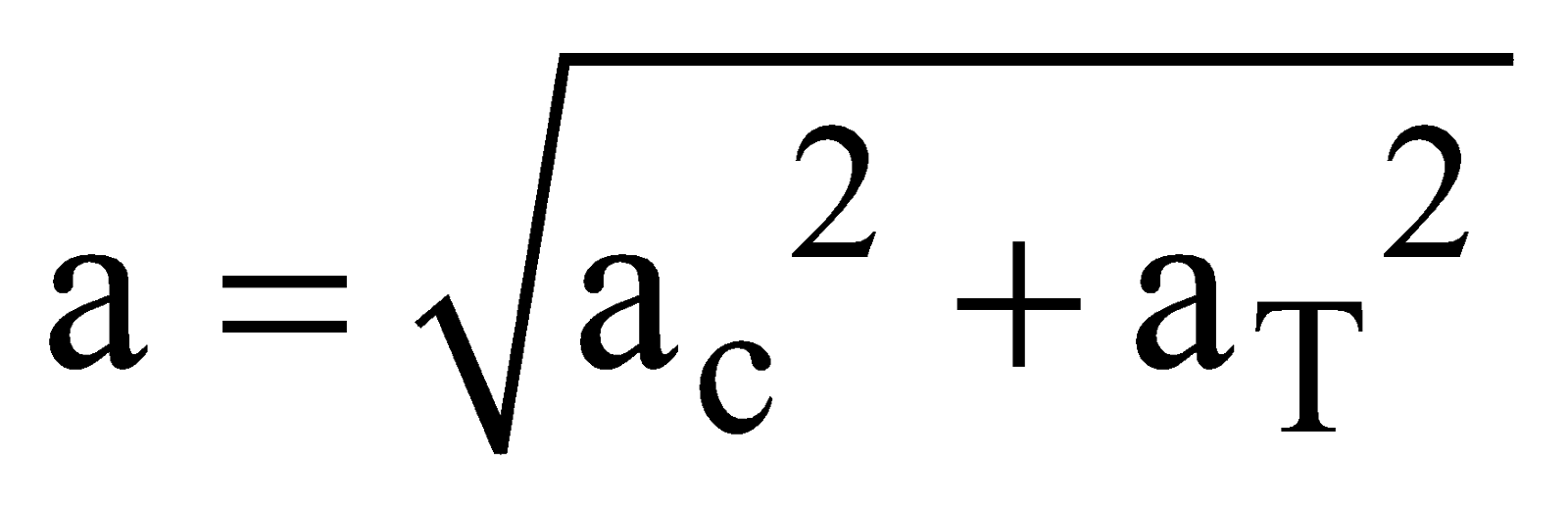
- If aT = 0 or α = 0, no work is done in circular motion.