7.3 The structure of matter
Essential Idea:
It is believed that all the matter around us is made up of fundamental particles called quarks and leptons. It is known that matter has a hierarchical structure with quarks making up nucleons, nucleons making up nuclei, nuclei and electrons making up atoms and atoms making up molecules. In this hierarchical structure, the smallest scale is seen for quarks and leptons (10–18m).
Understandings:
- Quarks, leptons and their antiparticles
- Hadrons, baryons and mesons
- The conservation laws of charge, baryon number, lepton number and strangeness
- The nature and range of the strong nuclear force, weak nuclear force and electromagnetic force
- Exchange particles
- Feynman diagrams
- Confinement
- The Higgs boson
Applications and Skills:
- Describing the Rutherford-Geiger-Marsden experiment that led to the discovery of the nucleus
- Applying conservation laws in particle reactions
- Describing protons and neutrons in terms of quarks
- Comparing the interaction strengths of the fundamental forces, including gravity
- Describing the mediation of the fundamental forces through exchange particles
Data booklet reference:
 |  |
 |
The structure of matter
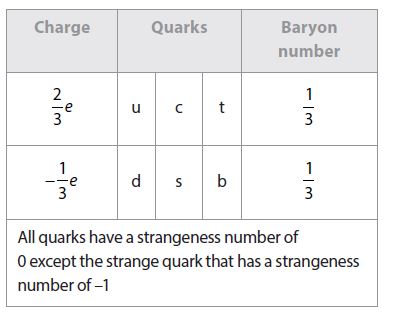
Particle properties
| Charge | Quarks | Baryon number | Charge | Leptons | |||||
| 2/3 e | u | c | t | 1/3 | -1 | e | μ | τ | |
| -1/3e | d | s | b | 1/3 | 0 | υe | υμ | υτ | |
| All quarks have a strangeness number of 0 except the strange quark that has a strangeness number of –1 | All leptons have a lepton number of 1 and antileptons have a lepton number of –1 | ||||||||
| Gravitational | Weak | Electromagnetic | Strong | ||||||
| Particles experiencing | All | Quarks, leptons | Charged | Quarks, gluons | |||||
| Particles mediating | Graviton | W+, W-, Z0 | γ | Gluons | |||||
The properties of matter are based on substructures called molecules and atoms. Atoms have the substructure of a nucleus with orbiting electrons, the interactions of which explain atomic properties. Protons and neutrons, the interactions of which explain the stability and abundance of elements, form the substructure of nuclei. Protons and neutrons are not fundamental—they are composed of quarks. Like electrons and a few other particles, quarks may be the fundamental building blocks of all there is, lacking any further substructure. But the story is not complete, because quarks and electrons may have substructure smaller than details that are presently observable.
Yukawa particle.
Classification of particles – the standard model
The Standard Model came about through a combination of experimental discoveries and theoretical developments.
The model suggests that the only fundamental particles are leptons, quarks, and gauge bosons. All other particles are believed to consist of combinations of quarks and antiquarks.
concepts of particle production and annihilation and apply the conservation laws to these processes.
Every known particle has an associated anti-particle. That is a particle that has all the opposite quantum numbers, electric charge, lepton or baryon number, strangeness etc. As far as we know anti-matter does not have negative mass and still falls down. Tests have been done to see if anti-matter “falls up.” No conclusion test has been done to show that anti-matter falls up.

When a particle and its associated antiparticle collide they completely and totally annihilate turning into pure energy, in accordance to Einstein’s relation of E = mc2. An example of this is the annihilation of an electron and a positron (positively charged electron, basically). When they collide their mass is turned into energy in the form of two high energy gamma rays. During the annihilation mass-energy and momentum are conserved.
If a photon has a higher energy than the rest mass of the electron and positron, it is possible for a electron and positron to be spontaneously created.
Three classes of fundamental particle
There are over 240 subatomic particles. We classify them by how they interact with forces. There are 3 classes of observed particles.
| Class of Particle | Description | Example |
| Lepton | Fundamental particles. Not effected by the strong force. There are 3 particles and associated neutrinos. Leptons are not affected by the strong force. Leptons appear to have no geometrical size, but they do have mass. | Electron, Muon, Tau, Electron Neutrino, Muon Neutrino, and Tau Neutrino |
| Hadron | Particles affected by the strong force. They are made up of quarks. Include Baryons and Mesons. | Protons, Neutrons and Pions. |
| Exchange Boson | Fundamental particles that are exchanged between other particles. The exchange is the force. | Gluon, W & Z, Photon, Graviton |
Leptons come in three families each with an associated neutrino:
| Lepton | Mass | Associated Neutrino |
| Electron | 0.000511 GeV | Electron Neutrino |
| Muon | 0.1066 GeV | Muon Neutrino |
| Tau | 1.777 GeV | Tau Neutrino |
Electrons, muons and tau particles all have the same electric charge, but different masses. Both the muon and tau particle are unstable and decay relatively fast. The mean life of a Muon is 10-6 seconds whereas the tau’s mean lifetime is only 10-12 seconds. Neutrinos are electrically neutral, as their name suggests, where or not neutrinos have mass is a topic of current research. Neutrinos are so plentiful and neutral that they can pass straight through the earth and you have millions going through your body as you read this.
In quantum physics there are many new properties that appear to be conserved. These new conservation laws were discovered experimentally and appear to hold true. One of the new conservation laws is the conservation of “Lepton number.” Neutron undergoes negative beta decay, it gives off an electron with a lepton number of 1 and anti-electron neutrino with a lepton number -1. Thus the lepton number is conserved.
Hadrons are spilt into two groups, Baryons and Mesons. Hadrons by definition are particles that are affected by the strong force. They are some times referred to as “strongly interacting particles.”
Baryons are hadrons that are made of three quarks. Neutrons and protons are two common examples of baryons. All baryons have spin ½. Protons are the only baryons that are stable. Neutrons by themselves will break down, by beta negative decay, into protons. A neutron has a half life on the order of a 608 seconds and is relatively stable. There are baryons that are many times the mass of protons or neutrons but they all have very short half-lives and thus are not observed in daily life. Baryons that are heavier than nucleons are call hyperons.
Mesons are hadrons that are made of two quarks, one “normal” quark and an anti-matter quark. Mesons consist of pions, kaons, eta and several other particles. Mesons are responsible for mediating the strong force between hadrons or nucleons.
Quarks – Fundamental particles that make up all Hadrons. Quarks can come in three different colors and the respective anti-color, red, blue and green. The color charge is analogous to electric or mass charge. Color has nothing to do with the color as see by a human eye, physicists simply ran out of descriptive terms… Only “white combinations” are possible. In other words neutrons and protons have a red blue and green quark. Whereas mesons must have a quark of one color and a quark of the anti-color… Quarks are subject to the strong force via gluons, that literally glue the particle together.
In a Hadron the quarks are held together with gluons, however the gluons can not leave the Hadron, and thus the attraction between nucleons can not be due to gluons, but are in fact due to gluon exchanging quark pairs, or mesons.
| Quark | Charge | Mass |
| Up | +2/3 | 360 MeV |
| Down | -1/3 | 360 MeV |
| Charm | +2/3 | 1500 MeV |
| Strange | -1/3 | 540 MeV |
| Top | +2/3 | 174 GeV |
| Bottom | -1/3 | 5 GeV |
structure of nucleons in terms of quarks
Since nucleons are baryons they are made of three quarks. The table below shows the combination of quarks that makes up protons and neutrons. They differ by only one quark. All matter in the world around you is made of up and down quarks in combination with leptons. When a proton or neutron undergoes beta decay one of the quark changes flavor. The weak nuclear force is the only force that can change the flavor of a quark.
| Nucleon | Quark Configuration |
| Proton | uud |
| Neutron | udd |
four fundamental interactions
| Force | Exchange Particle |
| Gravity | Graviton |
| Weak Force | W+, W- & Z |
| Electromagnetic | Photon |
| Strong | Gluon, pions, mesons |
| Color | Gluon |
The strong force can be seen as an extension of the color force beyond the confines of the quarks or nucleon. In order of relative strength, weakest to strongest:
Gravity < Weak Force < Electromagnetic < Strong
In recent years the weak force and electromagnetic force were shown to be the same fundamental force, which has been called the electroweak force. Work is under way to theoretically or mathematically combine all four forces into one force, so that all phenomena can be explained by one force!
Feynman Diagrams
There are four fundamental forces in nature. They are:
- Electromagnetic Force
- Gravitational Attraction
- Strong Interaction
- Weak Interaction
Richard Feynman came up with a graphical representation of interactions, while taking into account the exchange particle or force carrier particle that plays the crucial role in them.
Feynman diagrams use a series of lines and vertices to illustrate the particle interactions. In addition, a wiggly line is used to represent the exchange particle. At each vertex, the following must be conserved:
- Charge
- Lepton Number
- Baryon Number
- Momentum
- Energy
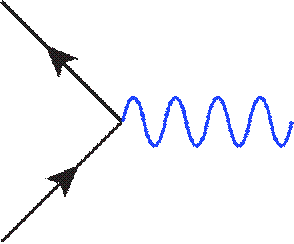
Now, let’s look at a simple Feynman diagram. It shows the electromagnetic force of repulsion between two electrons:
- The vertical axis represents time and the horizontal axis represents space.
- The total charge at both vertices remains -2.
- The first electron releases a photon to be received by the second electron, which in turn creates the force of repulsion.
- The momentum and energy are conserved. So are the baryon number and lepton numbers.
The strong force is held responsible for binding quarks together to form protons, neutrons and other (relatively) heavy particles. This is a short-range force which becomes insignificant at particle separations greater than \(10^-{15 } \) m. The nuclear force between nucleons is thought to be a residual effect of the much stronger force holding quarks together within each nucleon.
The electromagnetic force binds electrons and protons within an atom, and its residual effect holds together the atoms in a molecule or in a solid. This is a comparatively long-range force, decreasing proportional to the square of the distance between charged particles.
The weak force is a very short-range force (acting over distances \( 10^{-18}\) m which is involved in beta-decay and decay of some elementary particles such as the neutron. It is now believed that weak and electromagnetic forces are manifestations of a single electroweak force.
The gravitational force is a long-range inverse-square force which is negligible in the realm of atomic, nuclear and particle physics but which becomes the dominant force of attraction between large electrically-neutral objects separated by large distances, such as planets, stars and galaxies.
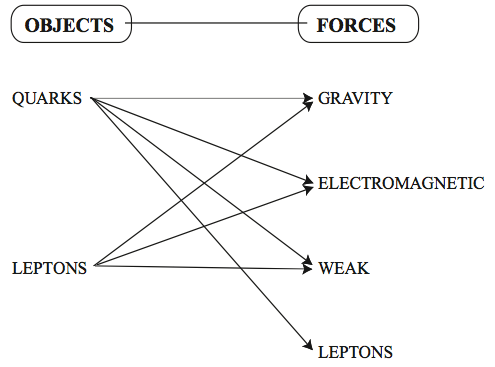
Particles can be classified in term of the interactions they take part in:
The electron and proton have charge so take part in electromagnetic interactions.
The proton and neutron are nucleons so take part in nuclear interactions.
The neutrino only takes part in weak interactions (beta decay).
Application of Conservation Laws
All particle interactions must obey a set of conservation laws. These are conservation of:
- Charge, Q
- Baryon number, B
- Lepton Number, L
- Strangeness, S
- Energy (or mass-energy)
- Momentum
- However, strangeness does not need to be conserved in weak interactions. It can change by either 0, +1 or –1
- Quantum numbers such as Q, B, L and S can only take discrete values (ie. 0, +1, –1, 1/2)
- To know whether a particle interaction can occur, check whether each quantum number is equal on both sides of the equation
- If even one of them, apart from strangeness in weak interactions, is not conserved then the interaction cannot occur
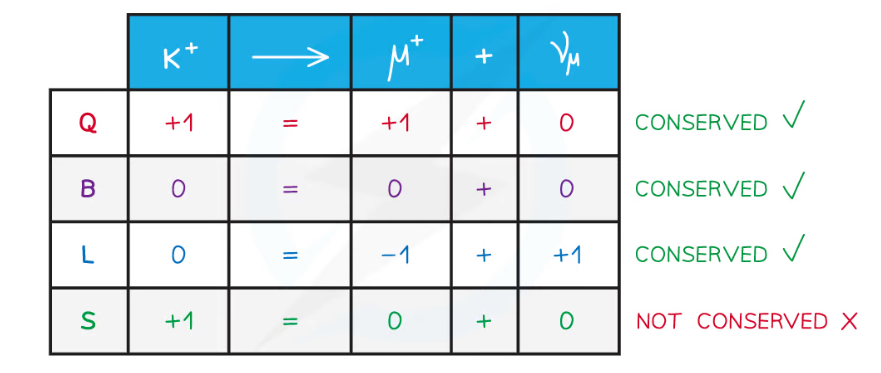
Baryon Number Conservation
This law requires that the total baryon number of a reaction is the same before and after the reaction occurs. To determine the total baryon number, every elementary particle is assigned a baryon number \(B\). The baryon number has the value \(B=1\) for baryons, \(B=-1\) for antibaryons, and 0 for all other particles.
Lepton Number Conservation
Lepton number conservation states that the sum of lepton numbers before and after the interaction must be the same. There are three different lepton numbers: the electron-lepton number \(L_e\), the muon-lepton number \(L_{\mu}\) and the tau-lepton number \(L_{\tau}\). In any interaction, each of these quantities must be conserved separately. For electrons and electron neutrinos, \(L_e =1\); for their antiparticles, \(L_e =-1\); all other particles have \(L_e =0\). Similarly, \(L_{\mu}=1\) for muons and muon neutrinos, \(L_{\mu}=-1\) for their antiparticles, and \(L_{\mu}=0\) for all other particles. Finally, \(L_{\tau}=1\),\(L_{\tau}=-1\) or \(L_{\tau}=0\) depending on whether we have a tau or tau neutrino, their antiparticles, or any other particle, respectively. Lepton number conservation guarantees that the number of electrons and positrons in the universe stays relatively constant. (Note: The total lepton number is, as far as we know, conserved in nature. However, observations have shown variations of family lepton number (for example,\(L_e\)) in a phenomenon called neutrino oscillations.)
The baryon number for several common particles is given in Table below.
| Particle name | Symbol | Lepton number (Le) | Lepton number (Lμ) | Lepton number (Lτ) | Baryon number (B) | Strange-ness number |
|---|---|---|---|---|---|---|
| Electron | e− | 1 | 0 | 0 | 0 | 0 |
| Electron neutrino | νe | 1 | 0 | 0 | 0 | 0 |
| Muon | μ− | 0 | 1 | 0 | 0 | 0 |
| Muon neutrino | νμ | 0 | 1 | 0 | 0 | 0 |
| Tau | τ− | 0 | 0 | 1 | 0 | 0 |
| Tau neutrino | ντ | 0 | 0 | 1 | 0 | 0 |
| Pion | π+ | 0 | 0 | 0 | 0 | 0 |
| Positive kaon | K+ | 0 | 0 | 0 | 0 | 1 |
| Negative kaon | K− | 0 | 0 | 0 | 0 | –1 |
| Proton | p | 0 | 0 | 0 | 1 | 0 |
| Neutron | n | 0 | 0 | 0 | 1 | 0 |
| Lambda zero | Λ0 | 0 | 0 | 0 | 1 | –1 |
| Positive sigma | Σ+ | 0 | 0 | 0 | 1 | –1 |
| Negative sigma | Σ− | 0 | 0 | 0 | 1 | –1 |
| Xi zero | Ξ0 | 0 | 0 | 0 | 1 | –2 |
| Negative xi | Ξ− | 0 | 0 | 0 | 1 | –2 |
| Omega | Ω− | 0 | 0 | 0 | 1 | –3 |
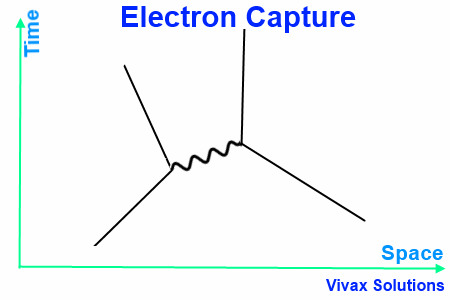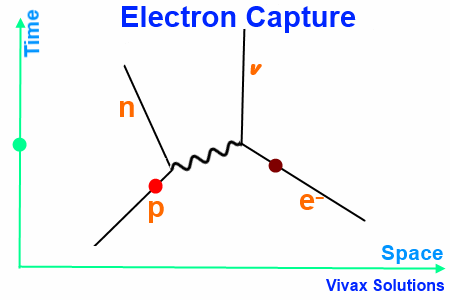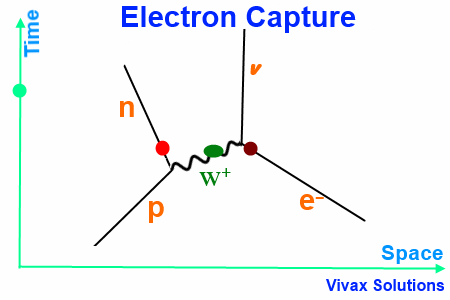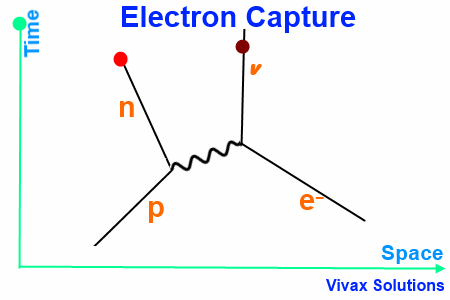
Electron Capture
Election Capture takes place when a proton from a proton-rich nucleus interact with an electron in an inner shell of the atom, just outside the nucleus.
W+ boson, the exchange particle, turns the electron into a neutrino.
Beta Decay
When a neutron or proton in an unstable nucleus emits a beta particle, the process is called beta decay. In both cases, the exchange particle is a W boson.
β– Decay
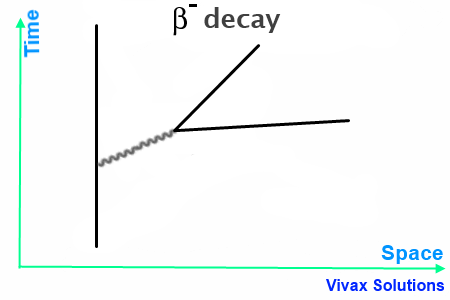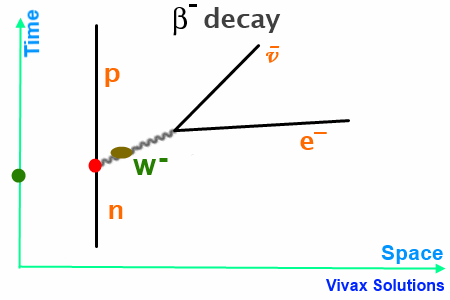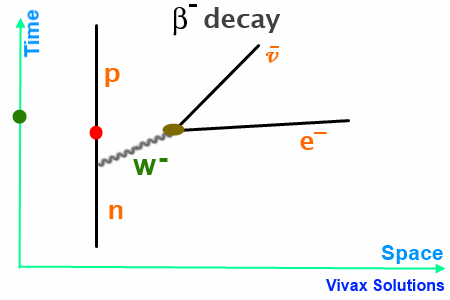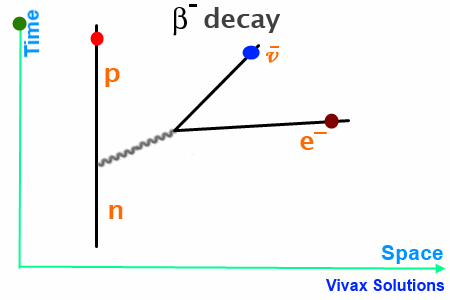
In this case, W–, released by the neutron, turns into an anti-neutrino and an electron – β– particle.
β+ Decay
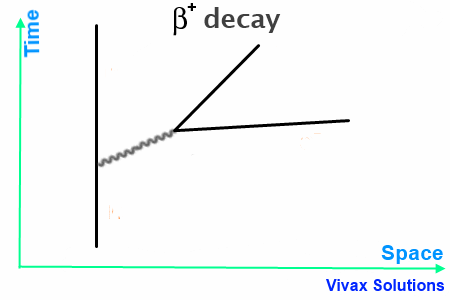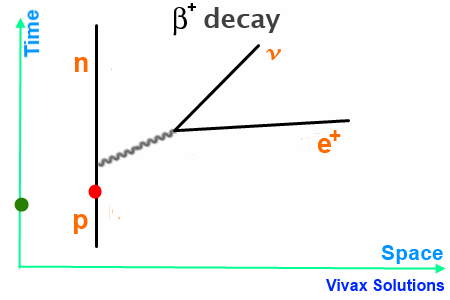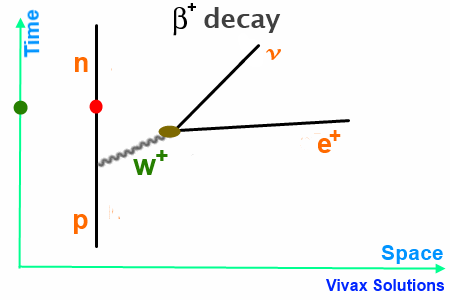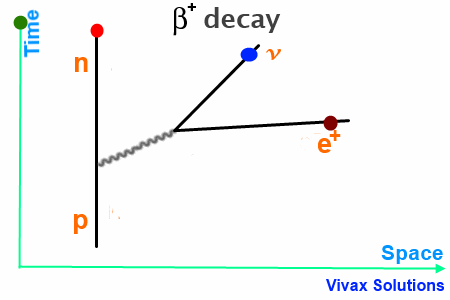
In this case, W+, released by the proton, turns into an neutrino and an positron – β+ particle.
Neutron-neutrino Interaction
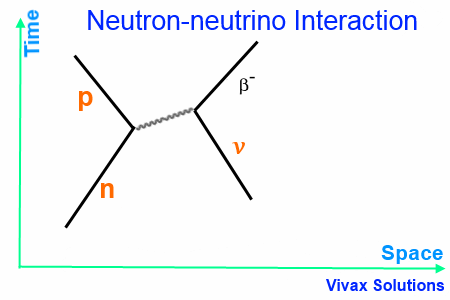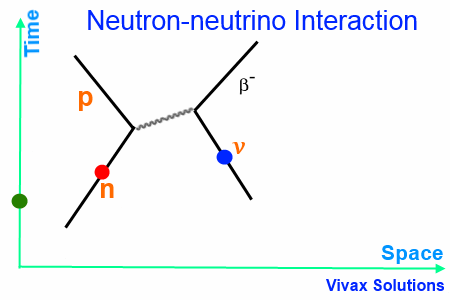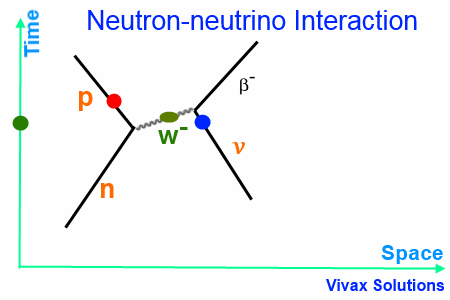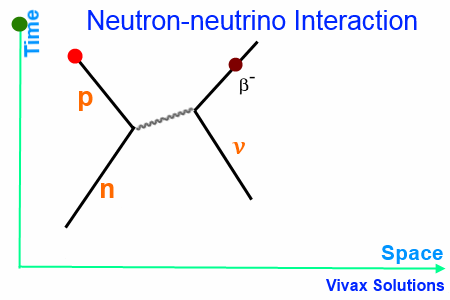
When a neutron interacts with a neutrino, a W– boson is released as the exchange particle, which in turn interacts with the neutrino to form the β– particle.
Proton-antineutrino Interaction
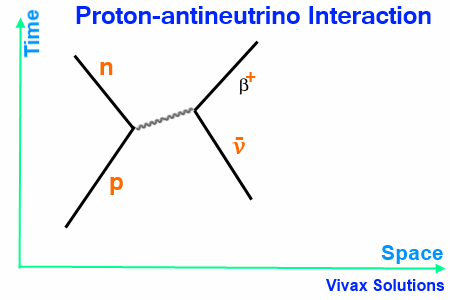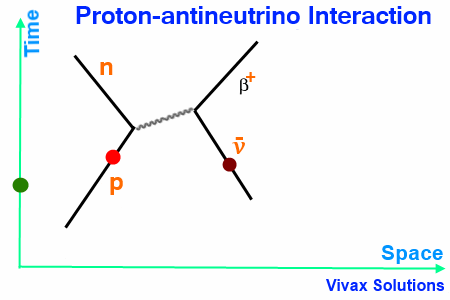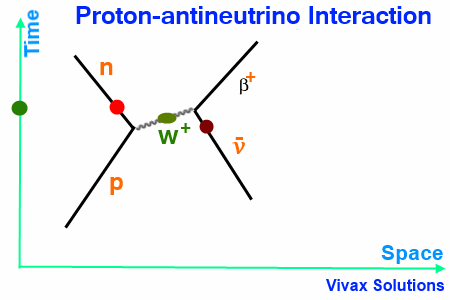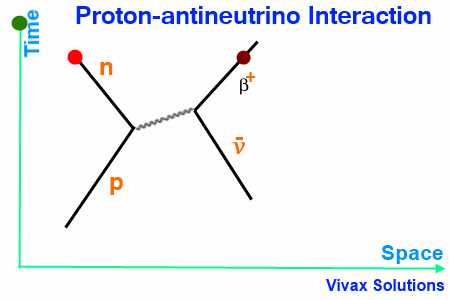
When a proton interacts with an antineutrino, a W+ boson is released as the exchange particle, which in turn interacts with the antineutrino to form the β+ particle.
Photons and W-bosons
Both photons and W-bosons are exchange particles or force carrier particles. Bosons, however, are different from photons, because,
- Bosons have non-zero rest mass.
- The range of bosons is less than 0.001 fm.
- Bosons are positively or negatively charged.
The Higgs boson
In the 1960s, Peter Higgs and, independently, Robert Brout and François Englert suggested that the mass discrepancy is due to a field (now called the Higgs
field) that permeates all of space and thus is a property of the vacuum.Without this field, the four messenger particles would be massless and indistinguishable—they would be symmetric.The Brout–Englert–Higgs theory demonstrates how the field breaks that symmetry, producing the electroweak messengers with one being massless. It also explains why all other particles, except for the gluon, have mass. The quantum of that field is the Higgs boson. Because of its pivotal role for all particles and because the theory behind its existence is compelling (even beautiful), intense searches for the Higgs boson were conducted on the Tevatron at Brookhaven and the Large Hadron Collider at CERN. In 2012, tantalizing experimental evidence was announced for the Higgs boson, at a mass of 125 GeV/c2.
Although we haven’t done all the mathematics, the particles of the standard model are all predicted by quantum mechanics. However, there is one piece that doesn’t fit. According to these predictions the W and Z bosons should not have any mass, but to fit in with the observation that the interactions are short range they must have large masses. One solution to this problem would be if the mass was not a property of the particle but a property of space. This is known as the Higgs field, and if there is a field there should be a particle associated with it, which we call the Higgs boson. A particle with these properties was detected in the ATLAS and CMS experiments at CERN on 4 July 2012.
Discovery of the neutrino
There are three nuclear decay processes where the atomic mass remains constant and the atomic number increases or decreases by one. They are all classified as beta decay, β. The first is β– decay where a neutron in the nucleus changes into a proton with the emission of an electron from the nucleus. The beta particle is the electron in this case. In β+ decay, a proton in the nucleus changes into a neutron and a positron (the beta particle) is released from the nucleus. With electron capture (EC) a proton in the nucleus changes into a neutron by capturing an atomic electron, usually from the inner shell. The isotopes on the neutron-rich side of the line of stability will tend to decay by β– emission, while those on the proton-rich side will most likely decay by β+ or electron capture.iv
The following reaction represents the β– decay of 210Bi.
210Bi → 210Po + e−
83 84
In this case the parent nucleus, 210Bi, decays into a daughter nucleus, 210Po, and an
83 84
electron (β– particle) is emitted. Notice that the atomic mass number, A, is the same for the parent and daughter nuclei. The β– decay has changed the balance of protons compared to neutrons in the daughter nucleus. We can calculate the amount of energy released in the decay by calculating the Q value for the reaction. The Q value is the difference between the rest energy of the parent nucleus and the sum of the rest energies of the products of the decay. In this case, the Q value is 1.16 MeV. The energy released by the decay should be seen as the kinetic energy of the emitted electron. This predicts that the kinetic energy of the electron should be the same each time this particular decay
takes place. However, experimentally, the energies of the electrons emitted in this beta decay are observed to vary from zero to the maximum energy available Emax= Q.
Figure 1 shows the energy spectrum of the electron emitted in this decay. The electrons is observed to have a range of kinetic energies, not one unique value as would be expected assuming energy, mass and momentum conservation.
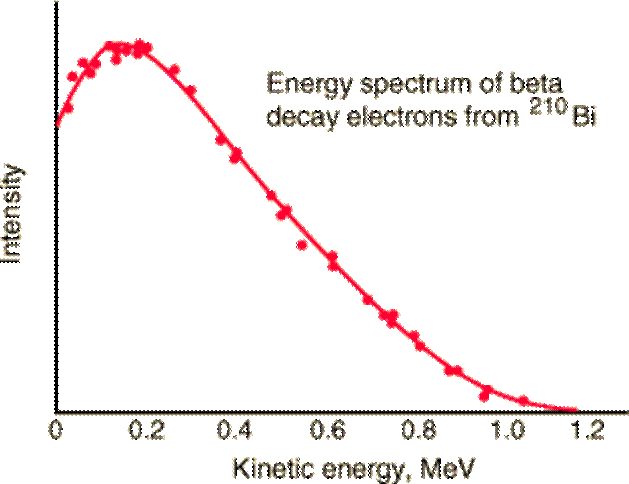 |
Figure 1. Experimental energy spectrum for decay electrons from Bismuth 210v The result is that in a particular β– decay event the electron carries away less
energy then the difference between the rest energy of the parent and daughter. This would result in energy and momentum not being conserved. The solution to this problem was first suggest by Wolfgang Pauli in 1930 when he proposed that a third particle was emitted in β– decay that carried the energy, linear and angular momentum necessary to conserve these quantities in each individual decay event. This new particle did not carry electric charge and had a mass much les than that of an electron. In 1933 Enrico Fermi developed a quantum theory of β– decay that incorporated this proposal and called the new particle the neutrino (“little neutral one” in Italian.) In 1956, in an experiment performed by Clyde Cowan and Frederick Reines, the first neutrinos were observed in the
laboratory. The decay of 210Bi now correctly written as
![]() 210Bi → 210Po + e− + 𝜐
210Bi → 210Po + e− + 𝜐
83 84
![]() Where the 𝜐 represents the neutrino (in this case is it antineutrino).vi
Where the 𝜐 represents the neutrino (in this case is it antineutrino).vi
Particle Zoo
Since the discovery of the electron neutrino, physicists have identified 13 fundamental constituents of matter. Just three of these-the up quark (u), the down quark (d), and the electron are needed to make protons and neutrons and to form atoms and molecules.
There are four fundamental forces that act in nature: the strong force, the weak force, the electromagnetic force and the gravitational force. The strong force is responsible for binding the particles in the nucleus (protons and neutron) together. The electromagnetic force binds electrons to the atomic nuclei to form atoms. The weak force helps the decay of heavy particles. The gravitational force acts between massive objects and has no roll on the subatomic scale. Particles transmit forces through exchange particles. Each force has its own exchange particle.vii
· The gluon mediates the strong forces; it “glues” quarks together
· The photon carries the electromagnetic force; it also transmits light
· The W and Z bosons represent the weak force; they induce different types of decays
Physicists suspect that the gravitational force may be associated with a boson particle hypothetically called the graviton.
Antimatter
For every particle that physicists have discovered a corresponding antiparticle exists. Antiparticles have the opposite properties of their corresponding particles. For example, an antiproton has a negative electric charge while a proton is positively charged. In the mid-1990’s physicists at CERN and Fermilab created the first anti-atoms, by carefully adding a positron and an antiproton to form antihydrogen. Storing antimatter is difficult task because as soon as an antiparticle and a particle meet they annihilate, disappearing in a flash of energy.viii
The Standard Model
Physicist call the framework that describes the interaction between elementary building blocks (quarks and leptons) and the force carriers (bosons) the Standard Model. Gravity is not yet part of this framework. The biggest success of the Standard Model is the unification of the electromagnetic and the weak forces into the electroweak force. This milestone is comparable to the unification of the electric and magnetic forces into a single theory by Maxwell in the 19th century.
Even though the Standard Model describes the interaction the sub atomic world, it does not explain the whole picture. The theory does not incorporate the gravitational force or explain questions such as what is dark matter. The Standard Model may only be a small part of a bigger picture and new information from experiments will continue to describe the functioning of the subatomic world.ix
 |
Table 1 The Standard Model of matter x
Quarks
There are six quarks grouped into three generations. All have fractional electric charge and distinct antiparticles. It is the quarks and antiquarks that bind together in multitude of ways to form more than 200 particles in the particle zoo and accounting for the vast majority of the visible mass of the universe. The bound states of the quarks and antiquarks are call hadrons and there are two subgroups of hadrons. Three group quark combinations are called baryons, which the proton and the neutron are the two most common examples and when a quark and antiquark combine they form mesons.xi
Leptons
There are three generations of leptons each consisting of a charged lepton and its related neutrino as shown in Table 1. The electron is the most familiar of the charged leptons and the only one that is stable. Each charged lepton has a distinct antiparticle and for each neutrino there is also an antineutrino although at this point in time it is possible that the
two are not distinct like the photon is its own antiparticle. Unlike the quarks there are not lepton-lepton bound states. Leptons are also referred to having three flavors: electron, muon, and tau.xii
Feynman diagrams
Feynman diagrams are space-time diagrams, that is, time (ct) versus space graphs, used to describe interaction of quarks, leptons and the mediator of these interactions. They are used to compute lifetimes and cross section for particle interaction events. The time (ct) and space (x) axes are normally not drawn but time (ct) is positive upward and generally drawn with time flowing horizontally toward the right as shown in Figure 2. Straight lines with an arrow represent particles. A particle line whose arrow points backward in time is interpreted as the corresponding antiparticle moving forward in time thus omitting the use of over-bars for antiparticles. The lines are symbolic and do not represent the particle trajectories. The diagrams show the interactions between particles and electromagnetic phenomena. Interactions occur at the vertices and photons are shown as a wiggly line.xiii
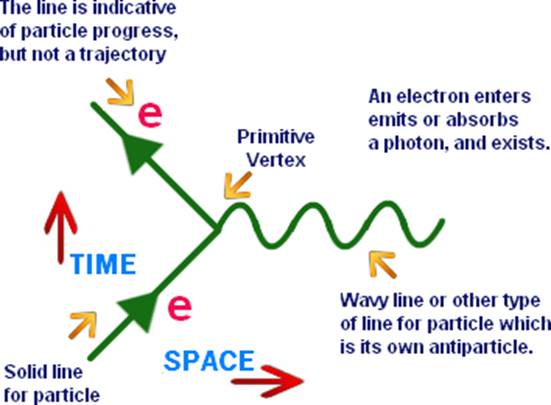 |
Figure 3 Feynman diagramxiv
Student activities
Appendix 2 has four student activities to aid them in understanding the nature and experimental background of particle physics. The first is a worksheet reviewing how to read a particle physics chart; the goal is to familiarize the students with the families of matter and their relationship with forces. The second, is a tutorial into how to draw Feynman diagrams adapted from quantum diaries website. After completion of this activity students should be able to draw eight required Feynman diagrams. The final two student activities are using actual experimental data. The first is to observe the tracks of particles in a bubble chamber. The second is to use actual data from a proton-proton collision to determine the mass of the top quark. These student activities are adapted from Topics in Modern Physics Particles by Leon Lederman Fermi lab group. Also included with student activities are teacher notes and answers to the student worksheet.
Appendix 1: Implementing Teaching Standards
The Structure of Matterxv
Predictions: Our present understanding of matter is called the Standard Model, consisting of six quarks and six leptons. Quarks were postulated on a completely mathematical basis in order to explain patterns in the properties of particles. It was much later that large-scale collaborative experimentation led to the discovery of the predicted fundamental particles.
Student should understand
· Quarks, leptons and their antiparticles.
· Hadrons, baryons and mesons.
· The conservation laws of charge, baryon number, lepton number and strangeness.
· The nature and range of the strong nuclear force, weak nuclear force and electromagnetic force
· Exchange particles
· Feynman diagrams
· Confinement
· The Higgs boson Students should be able to:
· Describe the Rutherford-Geiger-Marsden experiment that led to the discovery of the nucleus
· Applying conservation laws in particle reactions
· Describing protons and neutrons in terms of quarks
· Comparing the interaction strengths of the fundamental forces, including gravity
· Describing the mediation of the fundamental forces through exchange particles
· Sketching and interpreting simple Feynman diagrams
· Describing why free quarks are not observed
Appendix 2 Student Activities and Handouts
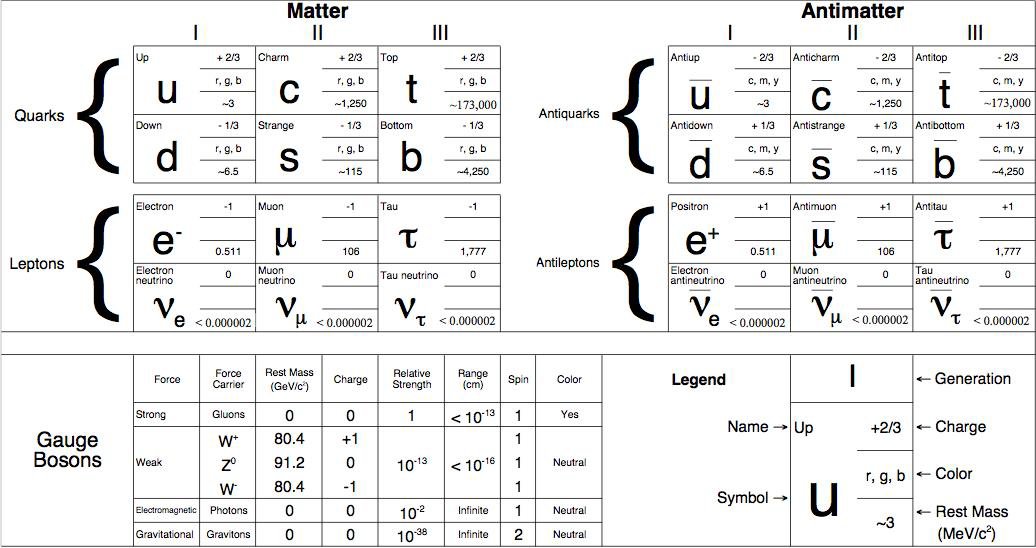
THE STANDARD MODEL OF ELEMENTARY PARTICLES CHART THE ULTIMATE PERIODIC TABLE WHAT CAN WE LEARN FROM IT?xvi
The purpose of this activity is to familiarize you with the Standard Model of Elementary Particles by studying the Standard Model of Elementary Particles Chart.
As you look at the Chart, you will see that it is divided into four sections. The two top sections list a total of 24 elementary particles. You will need information from these two sections to answer the following questions.
1. The two top sections are labeled and .
2. For the time being, let’s disregard the right hand side of the Chart and look at the left side labeled Matter. This category is further divided into two groups of six particles. These groups of particles are given the names and
3. List the flavors (names) of the six quarks.
4. List the flavors (names) of the six leptons.
5. The symbol for each quark is .
6. Using the Chart, write the symbols for the following particles:
up quark down quark top quark charm quark
7. Look at the leptons on the Chart. Their symbols (except for the electron) are Greek letters. Fill in the symbols below
Lepton | Symbol | Name of Greek letter |
|
|
|
|
|
|
|
|
|
Since there are three different neutrinos, how do their symbols distinguish them from one another?
Write the symbol for an electron neutrino:
8. Given the list of particles below, circle the quarks. (Do this without looking at the Chart if you can.)
up, neutrino, electron, down, tau, charm, strange
9. Using the legend in the lower right-hand corner of the Chart, write down the charge and approximate mass of each of the following:
Particle | Charge | Mass |
up |
|
|
strange |
|
|
top |
|
|
electron |
|
|
tau |
|
|
Electron neutrino |
|
|
10. Why can mass be measured in MeV/c2 ?
11. Using the Chart complete the following: have charges that are integers, and have charges that are fractions.
12. Baryons are particles that are made from quarks. The most common baryons are the neutron and the proton. Applying the law of conservation of charge (that is, no charge can be created or destroyed), what is the minimum number of quarks that must be joined to make up one baryon that has a charge of either +1, -1, or 0?
Show the proof of your answer here.
13. List three combinations of quarks that will give you a baryon with a charge of: a) +1 b) -1 c) 0
EXAMPLE: A baryon composed of ccs has a charge of +2/3 + 2/3 – 1/3 = +1. QUARK COMBINATIONS FOR: +1 -1 0
14. The quarks and leptons in column 1 of the Chart make up all the stable matter such as protons and neutrons. (Neutrons are stable relative to other particles, although they can decay.) Apply this information to write the quark configuration for a proton and for a neutron.
proton neutron
15. Which leptons are found in Column (or Family) I? Do you think these are stable too?
Now let’s look at the right side of the Chart, marked Antimatter. Using the Chart, explain how the antiparticles differ from the particles in:
a) Charge
b) Mass
c) Symbol
(Which particle is an exception?)
d) Color
An antibaryon is made from antiquarks. EXAMPLE: The antiquark configuration for an antiproton is uud since it has a charge of -1; strangeness = 0. Write the antiquark configuration for the following:
![]() Antineutron (h) Antisigma minus (S)
Antineutron (h) Antisigma minus (S)
Antiomega plus (W
The Chart in the bottom left-hand corner lists the Gauge bosons. These are the carriers of the four fundamental forces in nature. List the four forces and their carriers.
Force | Carrier |
|
|
|
|
|
|
|
|
1. Which particles are charged?
2. Which force has the shortest range?
3. Which force(s) is/are affected by the color?
4. Which force is the weakest?
5. Which force holds the quarks together to form baryons?
![]()
Answer Key
1. matter, antimatter
2. quarks, leptons
3. up, charm, top down, strange, bottom
4. electron, muon, tau electron neutrino, muon neutrino, tau neutrino
5. the first letter of its name
6. u, d, t, c
7. ![]() m t, n,subscript,n e
m t, n,subscript,n e
8. up, down, charm, strange
9. +2/3, 3 MeV/c2 -1/3, 115 MeV/c2 +2/3, 175,000 MeV/c2 -1, 0.511 MeV/c2 -1,
![]() 1784 MeV/c2 0, < 3 10-6 MeV/c2
1784 MeV/c2 0, < 3 10-6 MeV/c2
10. mass-energy equivalence
11. leptons, quarks
12. 3; two quarks will have a total charge of +1/3, +4/3, or -2/3.
13. Some of the possible combinations are: +1 (ucd, utb, ucs); -1 (dsb, dds, ddb); 0 (uds, cdb, tsb)
14. proton = uud, neutron = udd
15. electron, electron neutrino, yes
16. strong, gluons weak, W+, W–, Zo electromagnetic, photons gravity, gravitons
17. W+, W–
18. weak
19. strong
20. gravity
21. strong
How to draw Feynman Diagrams Adapted from Quantum Diariesxvii
For now, think of this as a game. You’ll need a piece of paper and a pen/pencil. The rules are as follows (read these carefully):
You can draw two kinds of lines, a straight line with an arrow or a wiggly line:

You can draw these pointing in any direction.
You may only connect these lines if you have two lines with arrows meeting a single wiggly line.
 |
Note that the orientation of the arrows is important! You must have exactly one arrow going into the vertex and exactly one arrow coming out. Your diagram should only contain connected pieces. That is every line must connect to at least one vertex. There shouldn’t be any disconnected part of the diagram.
What does it all mean?
Now we get to some physics.
Each line in rule (1) is called a particle.
The vertex in rule (2) is called an interaction.
The rules above are an outline for a theory of particles and their interactions. We called it QED, which is short for quantum electrodynamics.
The lines with arrows are matter particles (“fermions”).
The wiggly line is a force particle (“boson”), which, in this case, mediates electromagnetic interactions: it is the photon.
The diagrams tell a story about how a set of particles interacts.
We read the diagrams from left to right, so if you have up-and-down lines you should shift them a little so they slant in either direction. This left-to-right reading is important since it determines our interpretation of the diagrams.
Matter particles with arrows pointing from left to right are electrons.
Matter particles with arrows pointing in the other direction are positrons (antimatter). In fact, you can think about the arrow as pointing in the direction of the flow of electric charge. As a summary, we our particle content is: e+ is a positron, e- is an electron, and the gamma is a photon… think of a gamma ray.
From this we can make a few important remarks:
The interaction with a photon shown above secretly includes information about the conservation of electric charge: for every arrow coming in, there must be an arrow coming out.
But wait: we can also rotate the interaction so that it tells a different story. Here are a few examples of the different ways one can interpret the single interaction (reading from left to right):
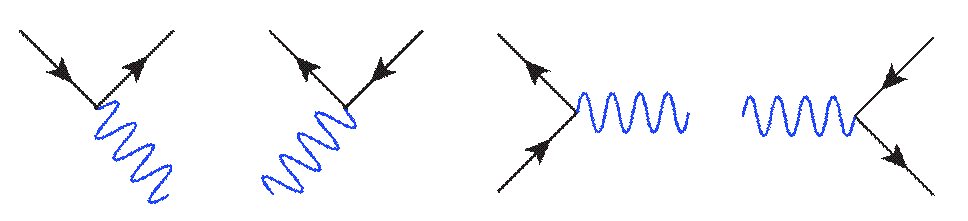
These are to be interpreted as: (1) an electron emits a photon and keeps going, (2) a positron absorbs a photon and keeps going, (3) an electron and positron annihilate into a photon, (4) a photon spontaneously “pair produces” an electron and positron.
On the left side of a diagram we have “incoming particles,” these are the particles that are about to crash into each other to do something interesting. For example, at the LHC these ‘incoming particles’ are the quarks and gluons that live inside the accelerated protons. On the right side of a diagram we have “outgoing particles,” these are the things which are detected after an interesting interaction.
For the theory above, we can imagine an electron/positron. In these experiments an electron and positron collide and the resulting outgoing particles are detected. In our simple QED theory, what kinds of “experimental signatures” (outgoing particle configurations) could they measure? (e.g. is it possible to have a signature of a single electron with two positrons? Are there constraints on how many photons come out?) So we see that the external lines correspond to incoming or outgoing particles. What about the internal lines? These represent virtual particles that are never directly
observed. They are created quantum mechanically and disappear quantum mechanically, serving only the purpose of allowing a given set of interactions to occur to allow the incoming particles to turn into the outgoing particles. Here is an example where we have a virtual photon mediating the interaction between an electron and a positron.
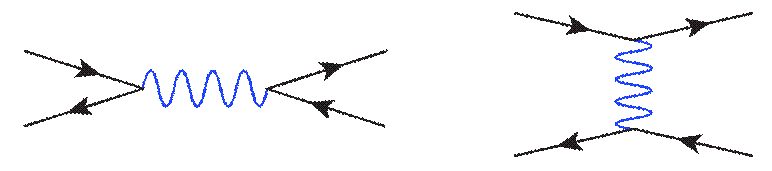
In the first diagram the electron and positron annihilate into a photon, which then produces another electron-positron pair. In the second diagram an electron tosses a photon to a nearby positron (without ever touching the positron). This creates a visual description of the idea that force particles are just quantum object that mediate forces. However, our theory treats force and matter particles on equal footing. We could draw diagrams where there are photons in the external state and electrons are virtual as shown below:
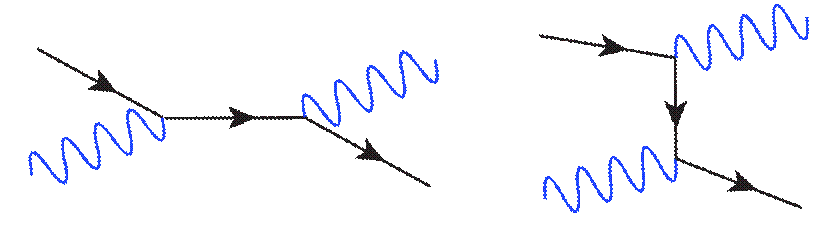
This is a process where light (the photon) and an electron bounce off each other and is called Compton Scattering. (1) that the electron emits a photon and then scatters off of the incoming photon, or (2) we can say that the incoming photon pair produced with the resulting positron annihilating with the electron to form an outgoing photon:
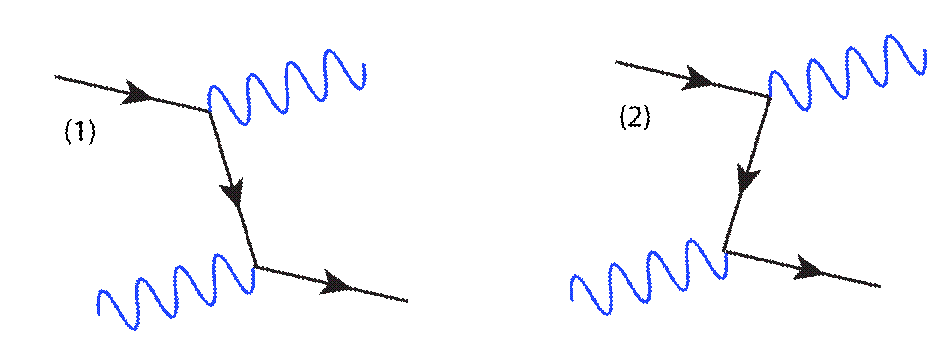
Anyway, this is the basic idea of Feynman diagrams. They allow us to write down what interactions are possible. There is a much more mathematical interpretation of these diagrams that produces the mathematical expressions that predict the probability of these interactions to occur, and so there is actually some rather complicated mathematics.
However, just like a work of art, it’s perfectly acceptable to appreciate these diagrams at face value as diagrams of particle interactions.
You should be able to draw Feynman diagrams for the following interactions;
1. Electron scattering
2. Beta decay
3. Pion decay
4. Electron positron annihilation
5. Pair production
6. Muon decay
7. Quark interactions
8. Photon -photon scattering
BUBBLE CHAMBER TRACK ANALYSIS
In this October, 1973 photo, 300 GeV protons are incident in the 30-inch hydrogen bubble chamber. The electron spirals are counter-clockwise. Therefore, clockwise deflection indicates a positive charge.
1. At point A we have a proton-proton interaction, which produces a π+ and many other particles.
2. The π+ moves to B, where it recoils from an elastic collision with a proton.
3. The recoiling π+ slows as it travels to C. At C it decays according to the reaction:
p+ ® m+ + nm
The lack of forward momentum beyond point C indicates μ the likelihood of a decay of a particle (π+ ), which was essentially at rest.
4. The μ+ produced at point C travels to point D. At D it decays according to the reaction:
m+ ® e+ + ne + nm
