Question
Chemical kinetics involves an understanding of how the molecular world changes with time.
A catalyst provides an alternative pathway for a reaction, lowering the activation energy, \({E_{\text{a}}}\).
Sketch graphical representations of the following reactions, for X \( \to \) products.
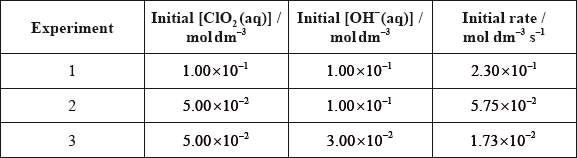
For the reaction below, consider the following experimental data.
\[{\text{2Cl}}{{\text{O}}_2}{\text{(aq)}} + {\text{2O}}{{\text{H}}^ – }{\text{(aq)}} \to {\text{ClO}}_3^ – {\text{(aq)}} + {\text{ClO}}_2^ – {\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}}\]
Another reaction involving \({\rm{O}}{{\rm{H}}^ – }\) (aq) is the base hydrolysis reaction of an ester.
\[{\text{C}}{{\text{H}}_3}{\text{COOC}}{{\text{H}}_2}{\text{CH(aq)}} + {\text{O}}{{\text{H}}^ – }{\text{(aq)}} \to {\text{C}}{{\text{H}}_3}{\text{CO}}{{\text{O}}^ – }{\text{(aq)}} + {\text{C}}{{\text{H}}_3}{\text{C}}{{\text{H}}_2}{\text{OH(aq)}}\]
A two-step mechanism has been proposed for the following reaction.
\[\begin{array}{*{20}{l}} {{\text{Step 1:}}}&{{\text{Cl}}{{\text{O}}^ – }{\text{(aq)}} + {\text{Cl}}{{\text{O}}^ – }{\text{(aq)}} \to {\text{ClO}}_2^ – {\text{(aq)}} + {\text{C}}{{\text{l}}^ – }{\text{(aq)}}} \\ {{\text{Step 2:}}}&{{\text{ClO}}_2^ – {\text{(aq)}} + {\text{Cl}}{{\text{O}}^ – }{\text{(aq)}} \to {\text{ClO}}_3^ – {\text{(aq)}} + {\text{C}}{{\text{l}}^ – }{\text{(aq)}}} \end{array}\]
(i) Define the term rate of reaction.
(ii) Temperature and the addition of a catalyst are two factors that can affect the rate of a reaction. State two other factors.
(iii) In the reaction represented below, state one method that can be used to measure the rate of the reaction.
\[{\text{ClO}}_3^ – {\text{(aq)}} + {\text{5C}}{{\text{l}}^ – }{\text{(aq)}} + {\text{6}}{{\text{H}}^ + }{\text{(aq)}} \to {\text{3C}}{{\text{l}}_2}{\text{(aq)}} + {\text{3}}{{\text{H}}_2}{\text{O(l)}}\]
(i) Define the term activation energy, \({E_{\text{a}}}\).
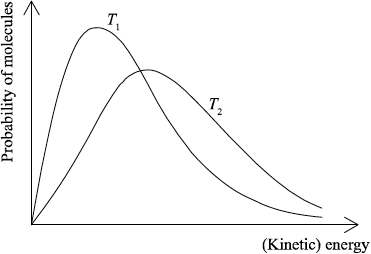
(ii) Sketch the two Maxwell–Boltzmann energy distribution curves for a fixed amount of gas at two different temperatures, \({T_1}\) and \({T_2}{\text{ }}({T_2} > {T_1})\). Label both axes.

(i) Concentration of reactant X against time for a zero-order reaction.
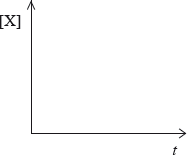
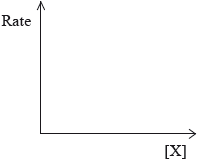
(ii) Rate of reaction against concentration of reactant X for a zero-order reaction.
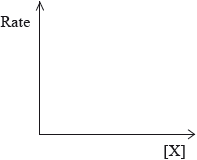
(iii) Rate of reaction against concentration of reactant X for a first-order reaction.
(i) Deduce the rate expression.
(ii) Determine the rate constant, \(k\), and state its units, using the data from Experiment 2.
(iii) Calculate the rate, in \({\text{mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{{\text{s}}^{ – 1}}\), when \({\text{[Cl}}{{\text{O}}_2}{\text{(aq)]}} = 1.50 \times {10^{ – 2}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) and \({\text{[O}}{{\text{H}}^ – }{\text{(aq)]}} = 2.35 \times {10^{ – 2}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\).
Apply IUPAC rules to name the ester, CH3COOCH2CH3(aq).
Describe qualitatively the relationship between the rate constant, k, and temperature, T.
The rate of this reaction was measured at different temperatures and the following data were recorded.
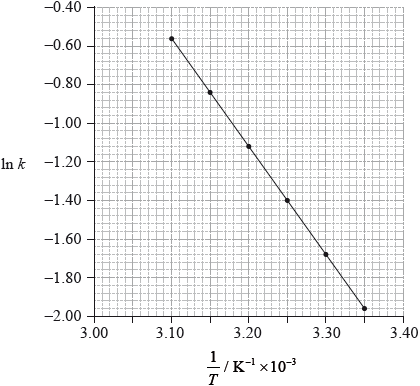
Using data from the graph, determine the activation energy, \({E_{\text{a}}}\), correct to three significant figures and state its units.
Deduce the overall equation for the reaction.
Deduce the rate expression for each step.
Step 1:
Step 2:
Answer/Explanation
Markscheme
(i) change in concentration of reactant/product with time / rate of change of concentration;
Increase can be used instead of change for product or decrease can be used instead of change for reactant.
Allow mass/amount/volume instead of concentration.
Do not accept substance.
(ii) concentration;
particle size / surface area;
light;
pressure;
Allow pH.
(iii) (measuring electrical) conductivity / (measuring) pH;
Accept other suitable method.
(i) minimum/least/smallest energy needed (by reactants/colliding particles) to react/start/initiate a reaction;
Allow energy difference between reactants and transition state.
Minimum/least/smallest required for the mark.
(ii) x-axis label: (kinetic) energy/(K)E and y-axis label: probability/fraction of molecules/particles / probability density;
Allow number of molecules/particles for y-axis.
correct shape of a typical Maxwell–Boltzmann energy distribution curve;
Do not award mark if curve is symmetric, does not start at zero or if it crosses x-axis.
two curves represented with second curve for \({T_2} > {T_1}\) to right of first curve, peak maximum lower than first curve and after the curves cross going to the right, \({T_2}\) curve needs to be above \({T_1}\) curve as illustrated;
M2 and M3 can be scored independently.
(i) 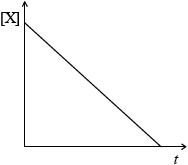 ;
;
(ii) 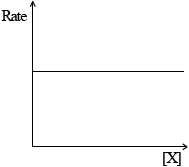 ;
;
(iii) 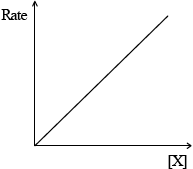 ;
;
(i) second order in \({\text{Cl}}{{\text{O}}_2}\) and first order in \({\text{O}}{{\text{H}}^ – }\);
rate \( = k{{\text{[Cl}}{{\text{O}}_{\text{2}}}{\text{]}}^2}{\text{[O}}{{\text{H}}^ – }{\text{]}}\);
Award [2] for correct final answer.
(ii) \(k = 2.30 \times {10^2}/230\);
\({\text{mo}}{{\text{l}}^{ – 2}}{\text{d}}{{\text{m}}^6}{{\text{s}}^{ – 1}}\);
(iii) \(1.22 \times {10^{ – 3}}/0.00122{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{{\text{s}}^{ – 1}}{\text{)}}\);
ethyl ethanoate;
Do not allow ethyl acetate.
as temperature/T increases, (value of) rate constant/k increases (exponentially);
Do not allow answers involving ln k from the Arrhenius equation.
Do not allow T directly proportional to k.
slope \( = – 5.6 \times {10^3}/ – 5600{\text{ (K)}}\);
\({E_{\text{a}}} = – {\text{slope}} \times {\text{R}}/{\text{slope}} = – {E_{\text{a}}}/R\);
\({E_{\text{a}}}{\text{(}} = 5.60 \times {10^3}{\text{ }}K \times 8.31{\text{ J}}\,{{\text{K}}^{ – 1}}{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}} = 4.65 \times {10^4}{\text{ (J}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}/46.5{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}\);
Accept answers in range 4.60 \( \times \) 104 J\(\,\)mol\(^{ – 1}\) to 4.67 \( \times \) \({10^4}\) (J mol \(^{ – 1}\)).
\({\text{J}}\,{\text{mo}}{{\text{l}}^{ – 1}}/{\text{kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\);
Accept J or kJ.
Unit mark can be scored independently but correct \({E_a}\) values with incorrect units scores only [3 max] (for example 46.5 J mol \(^{ – 1}\)).
Award [4] for correct final answer.
\({\text{3Cl}}{{\text{O}}^ – }{\text{(aq)}} \to {\text{ClO}}_3^ – {\text{(aq)}} + {\text{2C}}{{\text{l}}^ – }{\text{(aq)}}\);
Ignore state symbols.
Step 1: rate \( = k{{\text{[Cl}}{{\text{O}}^ – }{\text{]}}^{\text{2}}}\);
Step 2: rate \( = k{\text{[ClO}}_2^ – {\text{][Cl}}{{\text{O}}^ – }{\text{]}}\);
Penalize missing k once only.
Examiners report
This was the most popular question in Section B of the paper. Part (a) was very well answered.
In (b) (i), some candidates failed to mention minimum/least/smallest energy in the definition of activation energy. In part (ii), again candidates often dropped easy marks here for poor representations of the Maxwell-Boltzmann energy distribution curves. In some cases the curves were drawn symmetrically, which was incorrect. In addition, incorrect labels were often given for the x- and y-axes. Some candidates mixed these curves up with enthalpy level diagrams. It was nice to see more candidates giving a more precise label for the y-axis as probability/fraction of molecules rather than just number of molecules. The latter was allowed but is less precise (although does tend to be used in many IB textbooks).
Part (c) however was very well answered.
In part (d), many candidates also scored highly though the units of k in (ii) did cause a problem for some candidates.
In (e) (i), the most common mistake was candidates stating ethyl methanoate instead of ethyl ethanoate.
In part (ii), a number of candidates stated incorrectly that T is directly proportional to k, which is incorrect. Proportionality is a concept embedded in AS 11.3.1 in Topic 11, and may be worth some further discussion in the light of the Arrhenius Equation.
The most difficult part of Q6 however involved (e) (iii). Very few candidates scored full marks here and simply did not know how to manipulate the equation to get the activation energy. Others even gave incorrect units.
One respondent stated that part (f) (ii) would be difficult for candidates. (f) certainly did prove challenging and the rate expression for step two was often given incorrectly. This question became a good discriminating question in Section B. However the better students did manage to score all three marks in part (f).
One respondent stated that part (f) (ii) would be difficult for candidates. (f) certainly did prove challenging and the rate expression for step two was often given incorrectly. This question became a good discriminating question in Section B. However the better students did manage to score all three marks in part (f).
Question
Phosphine (IUPAC name phosphane) is a hydride of phosphorus, with the formula PH3.
(i) Draw a Lewis (electron dot) structure of phosphine.
(ii) State the hybridization of the phosphorus atom in phosphine.
(iii) Deduce, giving your reason, whether phosphine would act as a Lewis acid, a Lewis base, or neither.
(iv) Outline whether you expect the bonds in phosphine to be polar or non-polar, giving a brief reason.
(v) Phosphine has a much greater molar mass than ammonia. Explain why phosphine has a significantly lower boiling point than ammonia.
(vi) Ammonia acts as a weak Brønsted–Lowry base when dissolved in water.
![]()
Outline what is meant by the terms “weak” and “Brønsted–Lowry base”.
Weak:
Brønsted–Lowry base:
Phosphine is usually prepared by heating white phosphorus, one of the allotropes of phosphorus, with concentrated aqueous sodium hydroxide. The equation for the reaction is:
![]()
(i) The first reagent is written as P4, not 4P. Describe the difference between P4 and 4P.
(ii) The ion H2PO2− is amphiprotic. Outline what is meant by amphiprotic, giving the formulas of both species it is converted to when it behaves in this manner.
(iii) State the oxidation state of phosphorus in P4 and H2PO2−.
P4:
H2PO2−:
(iv) Oxidation is now defined in terms of change of oxidation number. Explore how earlier definitions of oxidation and reduction may have led to conflicting answers for the conversion of P4 to H2PO2− and the way in which the use of oxidation numbers has resolved this.
2.478 g of white phosphorus was used to make phosphine according to the equation:![]()
(i) Calculate the amount, in mol, of white phosphorus used.
(ii) This phosphorus was reacted with 100.0 cm3 of 5.00 mol dm−3 aqueous sodium hydroxide. Deduce, showing your working, which was the limiting reagent.
(iii) Determine the excess amount, in mol, of the other reagent.
(iv) Determine the volume of phosphine, measured in cm3 at standard temperature and pressure, that was produced.
Impurities cause phosphine to ignite spontaneously in air to form an oxide of phosphorus and water.
(i) 200.0 g of air was heated by the energy from the complete combustion of 1.00 mol phosphine. Calculate the temperature rise using section 1 of the data booklet and the data below.
Standard enthalpy of combustion of phosphine, ![]()
Specific heat capacity of air = 1.00Jg−1K−1=1.00kJkg−1K−1
(ii) The oxide formed in the reaction with air contains 43.6% phosphorus by mass. Determine the empirical formula of the oxide, showing your method.
(iii) The molar mass of the oxide is approximately 285 g mol−1. Determine the molecular formula of the oxide.
(iv) State the equation for the reaction of this oxide of phosphorus with water.
(v) Suggest why oxides of phosphorus are not major contributors to acid deposition.
(vi) The levels of sulfur dioxide, a major contributor to acid deposition, can be minimized by either pre-combustion and post-combustion methods. Outline one technique of each method.
Pre-combustion:
Post-combustion:
Answer/Explanation
Markscheme
(i)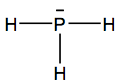
Accept structures using dots and/or crosses to indicate bonds and/or lone pair.
(ii)
sp3
Do not allow ECF from a (i).
(iii)
Lewis base AND has a lone pair of electrons «to donate»
(iv)
non-polar AND P and H have the same electronegativity
Accept “similar electronegativities”.
Accept “polar” if there is a reference to a small difference in electronegativity and apply ECF in 1 a (v).
(v)
PH3 has London «dispersion» forces
NH3 forms H-bonds
H-bonds are stronger
OR
London forces are weaker
Accept van der Waals’ forces, dispersion forces and instantaneous dipole – induced dipole forces.
Accept “dipole-dipole forces” as molecule is polar.
H-bonds in NH3 (only) must be mentioned to score [2].
Do not award M2 or M3 if:
• implies covalent bond is the H-bond
• implies covalent bonds break.
Accept “dipole-dipole forces are weaker”.
(vi)
Weak: only partially dissociated/ionized «in dilute aqueous solution»
Brønsted–Lowry base: an acceptor of protons/H+/hydrogen ions
Accept reaction with water is reversible/an equilibrium.
Accept “water is partially dissociated «by the weak base»”.
(i)
P4 is a molecule «comprising 4P atoms» AND 4P is four/separate «P» atoms
OR
P4 represents «4P» atoms bonded together AND 4P represents «4» separate/non-bonded «P» atoms
(ii)
can act as both a «Brønsted–Lowry» acid and a «Brønsted–Lowry» base
OR
can accept and/or donate a hydrogen ion/proton/H+
HPO22– AND H3PO2
(iii)
P4: 0
H2PO2–: +1
Do not accept 1 or 1+ for H2PO2−.
(iv)
oxygen gained, so could be oxidation
hydrogen gained, so could be reduction
OR
negative charge «on product/H2PO2 »/gain of electrons, so could be reduction
oxidation number increases so must be oxidation
Award [1 max] for M1 and M2 if candidate displays knowledge of at least two of these definitions but does not apply them to the reaction.
Do not award M3 for “oxidation number changes”.
(i)
«\(\left\langle {\frac{{2.478}}{{4 \times 30.97}}} \right\rangle \)»= 0.02000 «mol»
(ii)
n(NaOH) = «0.1000 × 5.00 =» 0.500 «mol» AND P4/phosphorus is limiting reagent
Accept n(H2O) = \(\frac{{100}}{{18}}\) = 5.50 AND P4 is limiting reagent.
(iii)
amount in excess «= 0.500 – (3 × 0.02000)» = 0.440 «mol»
(iv)
«22.7 × 1000 × 0.02000» = 454 «cm3»
Accept methods employing pV = nRT, with p as either 100 (454 cm3) or 101.3 kPa (448 cm3). Do not accept answers in dm3.
(i)
temperature rise «=\(\frac{{750 \times 1.00}}{{0.2000 \times 1.00}}\)»=3750«°C/K»
Do not accept −3750.
(ii)
n(P)«=\(\frac{{43.6}}{{30.97}}\)»=1.41 «mol»
n(O) «=\(\frac{{100 – 43.6}}{{16.00}}\)»=3.53 «mol»
«\(\frac{{n\left( {\rm{O}} \right)}}{{n\left( {\rm{P}} \right)}}\)=\(\frac{{3.53}}{{1.41}}\) = 2.50 so empirical formula is» P2O5
Accept other methods where the working is shown.
(iii)
«\(\frac{{285}}{{141.9}}\)=2.00, so molecular formula = 2×P2O5=»P4O10
(iv)
P4O10(s) + 6H2O (l) → 4H3PO4 (aq)
Accept P4O10(s) + 2H2O (l) → 4HPO3 (aq) (initial reaction)
Accept P2O5(s) + 3H2O(l) → 2H3PO4(aq)
Accept equations for P4O6/P2O3 if given in d (iii).
Accept any ionized form of the acids as the products.
(v)
phosphorus not commonly found in fuels
OR
no common pathways for phosphorus oxides to enter the air
OR
amount of phosphorus-containing organic matter undergoing anaerobic decomposition is small
Accept “phosphorus oxides are solids so are not easily distributed in the atmosphere”.
Accept “low levels of phosphorus oxide in the air”.
Do not accept “H3PO4 is a weak acid”.
(vi)
Pre-combustion:
remove sulfur/S/sulfur containing compounds
Post-combustion:
remove it/SO2 by neutralization/reaction with alkali/base
Accept “lime injection fluidised bed combustion” for either, but not both.
