Question
The properties of elements can be predicted from their position in the periodic table.
(i) Explain why Si has a smaller atomic radius than Al. [2]
(ii) Explain why the first ionization energy of sulfur is lower than that of phosphorus. [2]
Answer/Explanation
Ans
i
nuclear charge/number of protons/Z/Zeff increases «causing a stronger pull on the outer electrons»
same number of shells/«outer» energy level/shielding
ii
P has «three» unpaired electrons in 3p sub-level AND S has one full 3p orbital «and two 3p orbitals with unpaired electrons»
OR P: [Ne]3s23px 13py 13pz 1 AND S: [Ne]3s23px 23py13pz
repulsion between paired electrons in sulfur «and therefore easier to remove»
Accept orbital diagrams for 3p sub-level for M1. Ignore other orbitals or sub- levels. Accept “removing electron from S gives more stable half-filled sub-level” for M2.
Question
The Born-Haber cycle for MgO under standard conditions is shown below.
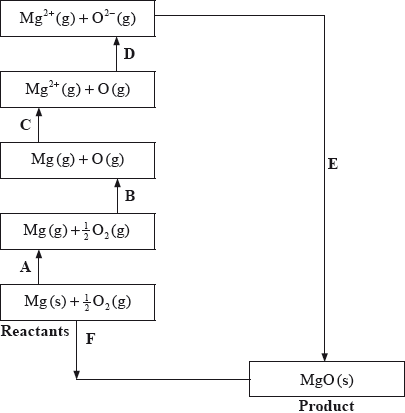
The values are shown in the table below.
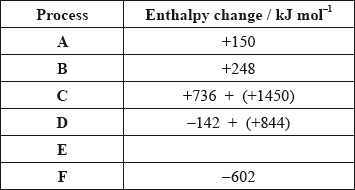
Identify the processes represented by A, B and D in the cycle.
Define the enthalpy change, F.
Determine the value of the enthalpy change, E.
Define the enthalpy change C for the first value. Explain why the second value is significantly larger than the first.
The inter-ionic distance between the ions in NaF is very similar to that between the ions in MgO. Suggest with a reason, which compound has the higher lattice enthalpy value.
The standard enthalpy change of three combustion reactions is given below in kJ.
\[\begin{array}{*{20}{l}} {{\text{2}}{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{6}}}{\text{(g)}} + {\text{7}}{{\text{O}}_{\text{2}}}{\text{(g)}} \to {\text{4C}}{{\text{O}}_{\text{2}}}{\text{(g)}} + {\text{6}}{{\text{H}}_{\text{2}}}{\text{O(l)}}}&{\Delta {H^\Theta } = – 3120} \\ {{\text{2}}{{\text{H}}_2}({\text{g)}} + {{\text{O}}_2}{\text{(g)}} \to {\text{2}}{{\text{H}}_2}{\text{O(l)}}}&{\Delta {H^\Theta } = – {\text{572}}} \\ {{{\text{C}}_2}{{\text{H}}_4}({\text{g)}} + {\text{3}}{{\text{O}}_2}{\text{(g)}} \to {\text{2C}}{{\text{O}}_2}{\text{(g)}} + 2{{\text{H}}_2}{\text{O(l)}}}&{\Delta {H^\Theta } = – {\text{1411}}} \end{array}\]
Based on the above information, calculate the standard change in enthalpy, \(\Delta {H^\Theta }\), for the following reaction.
\[{{\text{C}}_2}{{\text{H}}_6}({\text{g)}} \to {{\text{C}}_2}{{\text{H}}_4}({\text{g)}} + {{\text{H}}_2}{\text{(g)}}\]
Predict, stating a reason, whether the sign of \({\Delta {S^\Theta }}\) for the above reaction would be positive or negative.
Discuss why the above reaction is non-spontaneous at low temperature but becomes spontaneous at high temperatures.
Using bond enthalpy values, calculate \(\Delta {H^\Theta }\) for the following reaction.
\[{{\text{C}}_2}{{\text{H}}_6}({\text{g)}} \to {{\text{C}}_2}{{\text{H}}_4}({\text{g)}} + {{\text{H}}_2}{\text{(g)}}\]
Suggest with a reason, why the values obtained in parts (b) (i) and (b) (iv) are different.
Answer/Explanation
Markscheme
A: sublimation/atomization;
B: atomization/half dissociation enthalpy;
D: (sum of 1st and 2nd) electron affinity;
Do not accept vaporization for A and B.
Accept \(\Delta {H_{AT}}\)\( \cdot \) or \(\Delta {H_{EA}}\).
enthalpy change when one mole of the compound is formed from its elements (in their standard states);
under standard conditions / 25 °C/298 K and 1 atm/\({\text{101.3 kPa/1.01}} \times {\text{105 Pa}}\);
\( – 602 = 150 + 248 + 2186 + 702 + E\);
\( – {\text{3888 (kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}\);
Do not allow 3889 (given in data booklet).
Allow 3888 (i.e no minus sign).
Award [2] for the correct final answer.
energy required to remove one electron;
from an atom in its gaseous state;
electron removed from a positive ion;
decrease in electron-electron repulsion / increase in nucleus-electron attraction;
MgO;
double ionic charge / both ions carry +2 and –2 charge/greater charge compared to +1 and –1;
\[\begin{array}{*{20}{l}} {\left( {{{\text{C}}_2}{{\text{H}}_6}{\text{(g)}} + {\text{3}}\frac{1}{2}{{\text{O}}_2}{\text{(g)}} \to {\text{2C}}{{\text{O}}_2}{\text{(g)}} + {\text{3}}{{\text{H}}_2}{\text{O(l)}}} \right)}&{\Delta {H^\Theta } = – {\text{1560;}}} \\ {\left( {{{\text{H}}_2}{\text{O(l)}} \to {{\text{H}}_2}{\text{(g)}} + \frac{1}{2}{{\text{O}}_2}{\text{(g)}}} \right)}&{\Delta {H^\Theta } = + {\text{286;}}} \\ {\left( {{\text{2C}}{{\text{O}}_2}{\text{(g)}} + {\text{2}}{{\text{H}}_2}{\text{O(l)}} \to {{\text{C}}_2}{{\text{H}}_4}{\text{(g)}} + {\text{3}}{{\text{O}}_2}{\text{(g)}}} \right)}&{\Delta {H^\Theta } = + {\text{1411;}}} \\ {\left( {{{\text{C}}_2}{{\text{H}}_6}{\text{(g)}} \to {{\text{C}}_2}{{\text{H}}_4}{\text{(g)}} + {{\text{H}}_2}{\text{(g)}}} \right)}&{\Delta {H^\Theta } = + {\text{137 (kJ);}}} \end{array}\]
Allow other correct methods.
Award [2] for –137.
Allow ECF for the final marking point.
positive;
increase in number of moles of gas;
at low temperature, \({\Delta {H^\Theta }}\) is positive and \({\Delta G}\) is positive;
at high temperature, factor \({\text{T}}\Delta {S^\Theta }\) predominates and \({\Delta G}\) is negative;
Bonds broken (1C–C, 6C–H, or 1C–C, 2C–H) = 2825/1173;
Bonds made (1C=C, 1H–H, 4C–H) = 2700/1048;
+125 (kJ);
Allow 125 but not –125 (kJ ) for the final mark.
Award [3] for the correct final answer.
bond enthalpy values are average values;
Examiners report
This was the second most popular question and in general candidates demonstrated a good understanding of the Born Haber cycle. Some candidates identified the process A as vaporization instead of atomization.
Most candidates correctly stated the definition of enthalpy change of formation although some omitted to specify the standard conditions.
The majority of candidates correctly calculated the lattice enthalpy value.
The definition of the first ionization energy was stated correctly by most candidates but in a few cases the term gaseous state was missing.
The compound with higher lattice enthalpy was correctly identified including the reason.
The majority of candidates manipulated the thermo-chemical equations and calculated the correct answer of +137 kJ although some reversed the sign.
[N/A]
The explanation for why the reaction was non-spontaneous at low temperature but became spontaneous at high temperature was not always precise and deprived many candidates of at least one mark.
The bond enthalpy calculation had the usual mistakes of using the wrong value from the data booklet, bond making minus bond breaking and –125 kJ instead of +125 kJ.
Question
The periodic table shows the relationship between electron configuration and the properties of elements and is a valuable tool for making predictions in chemistry.
The ten elements in the first-row d-block have characteristic properties and many uses.
Define the term electronegativity.
(i) Outline two reasons why a sodium ion has a smaller radius than a sodium atom.
(ii) Explain why the ionic radius of \({{\text{P}}^{3 – }}\) is greater than the ionic radius of \({\text{S}}{{\text{i}}^{4 + }}\).
The graph below represents the successive ionization energies of sodium. The vertical axis plots log (ionization energy) instead of ionization energy to allow the data to be represented without using an unreasonably long vertical axis.
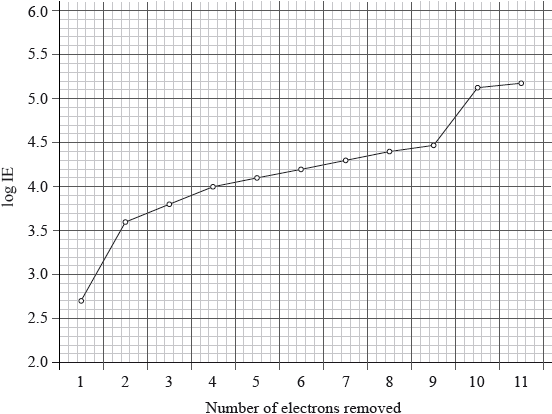
State the full electron configuration of sodium and explain how the successive ionization energy data for sodium are related to its electron configuration.
(i) Explain why the first ionization energy of aluminium is lower than the first ionization energy of magnesium.
(ii) Explain why the first ionization energy of sulfur is lower than the first ionization energy of phosphorus.
State and explain the type of reaction that takes place between \({\text{F}}{{\text{e}}^{3 + }}\) and \({{\text{H}}_{\text{2}}}{\text{O}}\) to form \({{\text{[Fe(}}{{\text{H}}_{\text{2}}}{\text{O}}{{\text{)}}_{\text{6}}}{\text{]}}^{3 + }}\) in terms of acid-base theories.
Explain why \({{\text{[Fe(}}{{\text{H}}_{\text{2}}}{\text{O}}{{\text{)}}_{\text{6}}}{\text{]}}^{3 + }}\) is coloured.
Outline the economic significance of the use of a catalyst in the Haber process which is an exothermic reaction.
Answer/Explanation
Markscheme
power/strength/ability of an atom to attract electrons/shared electron pair / OWTTE;
in a (covalent) bond;
Accept the word “element” in place of “atom”.
Do not accept electron (singular).
(i) Na: 11 p, 11/ 2.8.1 \({{\text{e}}^ – }\) and \({\text{N}}{{\text{a}}^ + }\): 11 p, 10 / 2.8 \({{\text{e}}^ – }\) / same number of protons, less electrons / \({\text{N}}{{\text{a}}^ + }\) has 2 shells/energy levels, Na has 3 / OWTTE;
Na+: has greater net positive charge/same number of protons pulling smaller number of electrons;
(ii) Si4+: 10 \({{\text{e}}^ – }\) in 2 (filled) energy levels / electron arrangement 2.8 / OWTTE;
P3−: 18 \({{\text{e}}^ – }\) in 3 (filled) energy levels / electron arrangement 2.8.8, thus larger / OWTTE;
OR
\({\text{S}}{{\text{i}}^{4 + }}\): has 2 energy levels where as \({{\text{P}}^{3 – }}\) has 3/ \({{\text{P}}^{3 – }}\) has one more (filled) energy
level;
\({\text{S}}{{\text{i}}^{4 + }}\): 10 \({{\text{e}}^ – }\) in 2 energy levels where as \({{\text{P}}^{3 – }}\) has 18 \({{\text{e}}^ – }\), thus larger;
\({\text{1}}{{\text{s}}^{\text{2}}}{\text{2}}{{\text{s}}^{\text{2}}}{\text{2}}{{\text{p}}^{\text{6}}}{\text{3}}{{\text{s}}^{\text{1}}}\);
Do not accept [Ne] 3s1.
first electron easy/easiest to remove / 1 electron in outermost/\({\text{n}} = 3\) energy level;
large increase between 1st and 2nd IE as electron now removed from \({\text{n}} = 2\) / next 8 electrons more difficult to remove / show (relatively) small increase as these electrons are in the same energy level/second energy level/\({\text{n}} = 2\);
large increase between 9th and 10th IE as electron now removed from n = 1 / 2
electrons very hard/most difficult to remove / innermost/lowest/closest to the nucleus/energy level/\({\text{n}} = 1\) / OWTTE;
electron 11 also comes from 1s, so shows a small increase;
(i) outer electron in Al is in 3p/p orbital/sub-shell/sub-level;
higher orbital/sub-shell / e– further from nucleus / shielded by 3s electrons;
(ii) in S, electron paired in 3p/p orbital/sub-shell/sub-level;
Accept extra stability associated with half filled p sub-shell (in P).
repulsion between paired electrons (and therefore easier to remove);
Lewis acid-base (reaction);
\({{\text{H}}_{\text{2}}}{\text{O}}\): e-pair donor, \({\text{F}}{{\text{e}}^{3 + }}\): \({{\text{e}}^ – }\) pair acceptor / \({{\text{H}}_{\text{2}}}{\text{O}}\) donates an electron pair to \({\text{F}}{{\text{e}}^{3 + }}\);
d sub-levels are split into two sets of orbitals (of different energies);
electron transitions between (d) orbitals of different energies / d-d transition(s);
transmitted (visible) light is complementary colour;
(exothermic reactions) low temperature/less energy increases ammonia yield;
(iron) catalyst used to increase rate of reaction / equilibrium reached faster / same yield but produced faster/in shorter/less time;
Examiners report
Generally, the definition of electronegativity was good, but some made the error of saying that it was the attraction of one electron only; others did not specify that it is the ability of an atom to attract a shared electron pair in a covalent bond.
Reasons why a sodium ion has a smaller radius than a sodium atom solicited incomplete answers. The answer requires the number of shells, electrons and protons of both the ion and the atom. Many candidates correctly said that \({\text{N}}{{\text{a}}^ + }\) had the same number of protons but one electron less so the pulling effect on the electrons was greater. Not many candidates gave the electronic structure or number of shells of the two ions, \({{\text{P}}^{3 – }}\) and \({\text{S}}{{\text{i}}^{4 + }}\), to explain their difference in ionic radius.
The graphical question on successive ionization energies of sodium was well answered by many. Typically, they explained how the successive ionization energies of sodium are related to its electron configuration from the data given. Most candidates realized that aluminium’s outer electron is in the 3p orbital so further from the nucleus and thus easier to ionize than magnesium. Similarly, sulfur has a paired electron in the 3p sub-shell and the repulsion between paired electrons is greater than in phosphorus which has a half filled p sub-shell.
Many candidates did not give sufficient answers to the part on transition elements. Some realised that it was a Lewis acid-base reaction where the electrons are donated by the water molecule to \({\text{F}}{{\text{e}}^{3 + }}\). Explanations given for the colour of complex ions continue to be muddled and the language used imprecise. Many wrote of “a split d orbital” rather than the d sub-level being split into two sets of orbitals (of different energies). The colour seen was often attributed to electrons emitting those wavelengths in transitions from higher energy to lower energy d orbitals rather than the transmitted visible light being the complementary colour of the one absorbed.
Few complete answers were given about economic significance of the use of a catalyst in the Haber process. A point that was missing often was that because the reaction is exothermic the forward reaction would be favoured (and the yield) if the temperature is lowered, but this would bring about a slower reaction so a catalyst is necessary to reach the equilibrium faster. However, there were misconceptions both in as far as catalysts and energetic is concerned. It was surprising to see the number of candidates who referred to activation energy but used the concept incorrectly. Few candidates established a connection with equilibrium.
Few complete answers were given about economic significance of the use of a catalyst in the Haber process. A point that was missing often was that because the reaction is exothermic the forward reaction would be favoured (and the yield) if the temperature is lowered, but this would bring about a slower reaction so a catalyst is necessary to reach the equilibrium faster. However, there were misconceptions both in as far as catalysts and energetic is concerned. It was surprising to see the number of candidates who referred to activation energy but used the concept incorrectly. Few candidates established a connection with equilibrium.
