Question
Hydrazine, N2H4, is a valuable rocket fuel.
The equation for the reaction between hydrazine and oxygen is given below.
\[{{\text{N}}_2}{{\text{H}}_4}({\text{l)}} + {{\text{O}}_2}({\text{g)}} \to {{\text{N}}_2}({\text{g)}} + 2{{\text{H}}_2}{\text{O(l)}}\]
The reaction between \({{\text{N}}_2}{{\text{H}}_4}({\text{aq)}}\) and \({\text{HCl(aq)}}\) can be represented by the following equation.
\[{{\text{N}}_2}{{\text{H}}_4}({\text{aq)}} + 2{\text{HCl(aq)}} \to {{\text{N}}_2}{\text{H}}_6^{2 + }({\text{aq)}} + 2{\text{C}}{{\text{l}}^ – }({\text{aq)}}\]
(i) Draw the Lewis (electron dot) structure for N2H4 showing all valence electrons.
(ii) State and explain the H–N–H bond angle in hydrazine.
Hydrazine and ethene, C2H4, are hydrides of adjacent elements in the periodic table. The boiling point of hydrazine is much higher than that of ethene. Explain this difference in terms of the intermolecular forces in each compound.
(i) The enthalpy change of formation, \(\Delta H_{\text{f}}^\Theta \), of liquid hydrazine is \({\text{50.6 kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\). Use this value, together with data from Table 12 of the Data Booklet, to calculate the enthalpy change for this reaction.
(ii) Use the bond enthalpy values from Table 10 of the Data Booklet to determine the enthalpy change for this reaction.
(iii) Identify the calculation that produces the most accurate value for the enthalpy change for the reaction given and explain your choice.
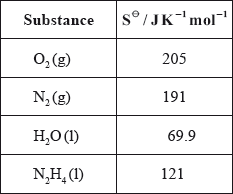
(iv) Calculate \(\Delta {S^\Theta }\) for the reaction using the data below and comment on its magnitude.
(v) Calculate \(\Delta {G^\Theta }\) for the reaction at 298 K.
(vi) Predict, giving a reason, the spontaneity of the reaction above at both high and low temperatures.
The reaction between \({{\text{N}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{(aq)}}\) and HCl(aq) can be represented by the following equation.
\[{{\text{N}}_2}{{\text{H}}_4}({\text{aq)}} + 2{\text{HCl(aq)}} \to {{\text{N}}_2}{\text{H}}_6^{2 + }({\text{aq)}} + 2{\text{C}}{{\text{l}}^ – }({\text{aq)}}\]
(i) Identify the type of reaction that occurs.
(ii) Predict the value of the H–N–H bond angle in \({{\text{N}}_{\text{2}}}{\text{H}}_{\text{6}}^{{\text{2}} + }\).
(iii) Suggest the type of hybridization shown by the nitrogen atoms in \({{\text{N}}_{\text{2}}}{\text{H}}_{\text{6}}^{{\text{2}} + }\).
Answer/Explanation
Markscheme
(i) 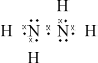 ;
;
Accept x’s, dots or lines for electron pairs
(ii) H–N–H \( < \) 109 / any angle between 104° and 109°;
due to four centres of electron charge / four electron pairs (one of which is a lone \({{\text{e}}^ – }\) pair);
extra repulsion due to lone electron pairs;
Do not allow ECF for wrong Lewis structures.
weaker van der Waals’/London/dispersion/intermolecular forces in ethene;
stronger (intermolecular) hydrogen bonding in hydrazine;
If no comparison between strengths then [1 max].
(i) \(\Delta H_{\text{r}}^\Theta = \Sigma \Delta H_{\text{f}}^\Theta {\text{ products}} – \Sigma \Delta H_{\text{f}}^\Theta {\text{ reactants}}\);
Can be implied by working.
\(\Delta H_{\text{f}}^\Theta {\text{(}}{{\text{H}}_2}{\text{O(l))}} = – 286{\text{ (kJ)}}\);
\(\Delta H_{\text{r}}^\Theta = 2( – 286) – 50.6 = – 622.6{\text{ (kJ)}}\);
(ii) bonds broken: 4N–H, N–N, O=O / \( + {\text{2220 (kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}\);
bonds formed: N\(\equiv\)N, 4O-H / \( – 2801{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}\);
\( – 581{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}\);
Award [3] for correct final answer.
(iii) value based on \(\Delta {H_{\text{f}}}\) more accurate;
\(\Delta {H_{\text{f}}}\) accurate for compounds in reaction;
bond energy calculation assumes average bond energies;
(bond energy calculation) only applies to gaseous states / ignores intermolecular bonds;
(iv) \(\Delta {S^\Theta } = \Sigma {S^\Theta }{\text{ (products)}} – \Sigma {S^\Theta }{\text{ (reactants)}}\);
Can be implied by working.
\( = 191 + (2 \times 69.9) – 205 – 121 = + 4.8{\text{ (J}}\,{{\text{K}}^{ – 1}}{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}\);
small value since number of mol of g on both sides the same;
(v) \(\Delta {G^\Theta } = – 622.6 – 298(0.0048)\);
\( = – 624.0{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}\);
Allow 623.9 to 624.1.
(vi) all reactions are spontaneous;
\(\Delta G\) is negative (at high temperatures and low temperatures);
(i) acid-base/neutralization;
(ii) 109°/109.5°;
(iii) sp3;
No ECF if bond angle incorrect in (ii).
Examiners report
The Lewis structure for hydrazine proved to be difficult for some in (a). Incorrect answers had double bonds appearing between the two nitrogen atoms or lone pairs missing. Those who could draw the correct structure in (i) gave the correct bond angle, but the explanation was often incomplete. Few mentioned either the four electron domains around the central atom or the extra repulsion of the lone pair.
In part (b) most candidates knew that hydrogen bonding was present in hydrazine and Van der Waals‟ forces in ethene but failed to give a comparison of the relative strength of the intermolecular forces.
Some candidates struggled to calculate the enthalpy changes from enthalpy changes of formation in (c) (i) as they were unable to relate the enthalpy change of combustion of hydrogen to the enthalpy change of formation of water.
The bond energy and entropy calculations were more successful with many candidates benefitting from ECF from their incorrect Lewis structures in (a). It was encouraging to see many correct unit conversions for the calculation of \(\Delta G\). A number of candidates incorrectly described the combination of hydrazine and hydrochloric acid as a redox reaction, but many were able to identify the bond angle and hybridization in \({{\text{N}}_{\text{2}}}{\text{H}}_{\text{6}}^{{\text{2}} + }\).
Question
In December 2010, researchers in Sweden announced the synthesis of N,N–dinitronitramide, \({\text{N(N}}{{\text{O}}_{\text{2}}}{{\text{)}}_{\text{3}}}\). They speculated that this compound, more commonly called trinitramide, may have significant potential as an environmentally friendly rocket fuel oxidant.
Methanol reacts with trinitramide to form nitrogen, carbon dioxide and water. Deduce the coefficients required to balance the equation for this reaction.
___ \({\text{N(N}}{{\text{O}}_2}{{\text{)}}_3}{\text{(g)}} + \) ___ \({\text{C}}{{\text{H}}_3}{\text{OH(l)}} \to \) ___ \({{\text{N}}_2}{\text{(g)}} + \) ___ \({\text{C}}{{\text{O}}_2}{\text{(g)}} + \) ___ \({{\text{H}}_2}{\text{O(l)}}\)
Calculate the enthalpy change, in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\), when one mole of trinitramide decomposes to its elements, using bond enthalpy data from Table 10 of the Data Booklet. Assume that all the N–O bonds in this molecule have a bond enthalpy of \({\text{305 kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\).
The entropy change, \(\Delta S\), for the decomposition of trinitramide has been estimated as \( + 700{\text{ J}}\,{{\text{K}}^{ – 1}}{\text{mo}}{{\text{l}}^{ – 1}}\). Comment on the sign of \(\Delta S\).
Using \( + 700{\text{ J}}\,{{\text{K}}^{ – 1}}{\text{mo}}{{\text{l}}^{ – 1}}\) as the value for the entropy change, along with your answer to part (c), calculate \(\Delta G\), in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\), for this reaction at 300 K. (If you did not obtain an answer for part (c), then use the value \( – 1000{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\), but this is not the correct value.)
Explain how changing the temperature will affect whether or not the decomposition of trinitramide is spontaneous.
Outline how the length of the N–N bond in trinitramide compares with the N–N bond in nitrogen gas, \({{\text{N}}_{\text{2}}}\).
Deduce the N–N–N bond angle in trinitramide and explain your reasoning.
Predict, with an explanation, the polarity of the trinitramide molecule.
Answer/Explanation
Markscheme
\(\underline {{\text{ (1) }}} {\text{N(N}}{{\text{O}}_2}{{\text{)}}_3}{\text{(g)}} + \underline {{\text{ 2 }}} {\text{C}}{{\text{H}}_3}{\text{OH(l)}} \to \underline {{\text{ 2 }}} {{\text{N}}_2}{\text{(g)}} + \underline {{\text{ 2 }}} {\text{C}}{{\text{O}}_2}{\text{(g)}} + \underline {{\text{ 4 }}} {{\text{H}}_2}{\text{O(l)}}\);
bonds broken: \((6 \times 305) + (3 \times 158) = 1830 + 474 = 2304{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}})\);
bonds made: \((2 \times 945) + (3 \times 498) = 1890 + 1494 = 3384{\text{ }}({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}})\);
enthalpy change: \(2304 – 3384 = – 1080{\text{ }}({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}})\);
Award [3] for correct final answer.
Award [2 max] for +1080 (kJ mol–1).
Accept –234 kJ mol–1 which arise from students assuming that 305 kJ mol–1 refers to the strength of a single N–O bond. Students may then take N=O from the data book value (587 kJ mol–1).
bonds broken: (3 \( \times \) 305) + (3 \( \times \) 587) + (3 \( \times \) 158) = 915 + 1761 + 474 = 3150 (kJ mol–1)
bonds made: (2 \( \times \) 945) + (3 \( \times \) 498) = 1890 + 1494 = 3384(kJ mol–1)
enthalpy change: 3150 – 3384 = –234(kJ mol–1).
Award [2 max] for correct calculation of the enthalpy change of reaction for the equation in part (a), which gives –2160 (kJ mol–1).
Award [1] if the final answer is not –2160 but the candidate has correctly calculated the bonds broken in trinitramide as 2304 (kJ mol–1).
increase in the number of moles of gas;
gases have a greater entropy/degree of randomness (than liquids or solids);
Award [1 max] for answers stating that positive value indicates an increase in disorder/randomness.
\(\Delta G = \Delta H – T \times \Delta S\);
\( = – 1080 – 300 \times \frac{{700}}{{1000}}\);
\( – 1290{\text{ }}({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}})\);
Award [3] for correct final answer.
Award [2 max] for incorrect conversions of units.
If no answer to part (c), using \(\Delta H\) = –1000 kJ mol–1, gives –1020 (kJ mol–1).
no change in spontaneity / temp has no effect on spontaneity / spontaneous at all temperatures;
\(\Delta G\) negative at all temperatures / exothermic/\(\Delta H\) negative and involves an increase in entropy/\(\Delta S\) positive;
(N–N bond in) trinitramide is longer/nitrogen (gas) is shorter / 0.145 nm in trinitramide versus 0.110 nm in nitrogen;
trinitramide has single (N–N) bond and nitrogen (gas) has triple bond;
106° – 108°;
Accept < 109°.
Any two for [2 max].
4 (negative) charge centres/electron pairs/electron domains around central nitrogen;
central nitrogen has a lone/non-bonding pair;
lone/non-bonding pairs repel more than bonding pairs;
molecule will be (trigonal/triangular) pyramidal;
(negative) charge centres/electron pairs/electron domains will be tetrahedrally arranged/orientated/ have tetrahedral geometry;
Do not apply ECF.
polar;
net dipole moment present in molecule / unsymmetrical distribution of charge / polar bonds do not cancel out / centre of negatively charged oxygen atoms does not coincide with positively charged nitrogen atom;
Marks may also be awarded for a suitably presented diagram showing net dipole moment.
Do not accept “unsymmetrical molecule”.
Apply ECF from part (h).
Examiners report
Most students could insert the coefficients to balance the equation provided and many recognized the benign nature of the products formed. Though the structure of trinitramide was not given this did not seem to hinder students in calculating the required enthalpy change. A worryingly high number of students however used bond enthalpies to calculate the enthalpy change in the part (a) equation rather than the much simpler decomposition asked for, so to allow them to gain some credit, the mark scheme was adjusted. The sections relating to entropy and free energy changes were generally well tackled, as was the comparative lengths of the N-N bonds. Predicting the shape and polarity of the trinitramide molecule often proved more difficult, especially explaining the polarity of the molecule. Explanations of the effect of external pressure on boiling point, in terms of vapour pressure, and of the effect of temperature, in terms of kinetic theory, often lacked clarity.
