Question
Methanol is made in large quantities as it is used in the production of polymers and in fuels. The enthalpy of combustion of methanol can be determined theoretically or experimentally.
\[{\text{C}}{{\text{H}}_3}{\text{OH(l)}} + {\text{1}}\frac{1}{2}{{\text{O}}_2}{\text{(g)}} \to {\text{C}}{{\text{O}}_2}{\text{(g)}} + {\text{2}}{{\text{H}}_2}{\text{O(g)}}\]
The enthalpy of combustion of methanol can also be determined experimentally in a school laboratory. A burner containing methanol was weighed and used to heat water in a test tube as illustrated below.
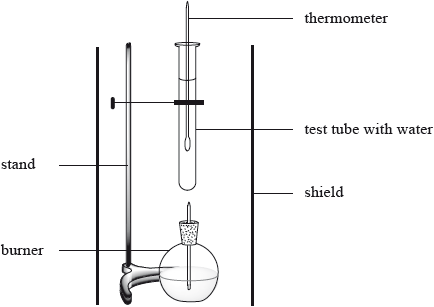
The following data were collected.

The Data Booklet value for the enthalpy of combustion of methanol is \( – {\text{726 kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\). Suggest why this value differs from the values calculated in parts (a) and (b).
Using the information from Table 10 of the Data Booklet, determine the theoretical enthalpy of combustion of methanol.
Calculate the amount, in mol, of methanol burned.
Calculate the heat absorbed, in kJ, by the water.
Determine the enthalpy change, in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\), for the combustion of 1 mole of methanol.
Part (a)
Part (b)
Answer/Explanation
Markscheme
amount of energy required to break bonds of reactants
\(3 \times 413 + 358 + 464 + 1.5 \times 498{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}/2808{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}\);
amount of energy released during bond formation of products
\(4 \times 464 + 2 \times 746{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}/3348{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}\);
\(\Delta H = – 540{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}\);
Award [3] for correct final answer.
Award [2] for (+)540.
If old Data Booklet is used accept answer: –535 (kJ\(\,\)mol–1) or award [2] for (+)535.
\(m{\text{(methanol)}} = (80.557 – 80.034) = 0.523{\text{ (g)}}\);
\(n{\text{(methanol)}} = \left( {\frac{{0.523{\text{ g}}}}{{32.05{\text{ g}}\,{\text{mo}}{{\text{l}}^{ – 1}}}}} \right) = 0.0163{\text{ (mol)}}\);
Award [2] for correct final answer.
\(\Delta T = (26.4 – 21.5) = 4.9{\text{ (K)}}\);
\(q = (mc\Delta T = ){\text{ }}20.000 \times 4.18 \times 4.9{\text{ (J)}}/20.000 \times 4.18 \times 4.9 \times {10^{ – 3}}{\text{ (kJ)}}\);
0.41 (kJ);
Award [3] for correct final answer.
\(\Delta H_{\text{c}}^\Theta = – \frac{{0.41{\text{ (kJ)}}}}{{0.0163{\text{ (mol)}}}}/ – 25153{\text{ (J}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}\);
\( = – 25{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}\);
Award [2] for correct final answer.
Award [1] for (+)25 (kJ\(\,\)mol–1).
bond enthalpies are average values/differ (slightly) from one compound to another (depending on the neighbouring atoms) / methanol is liquid not gas in the reaction;
not all heat produced transferred to water / heat lost to surroundings/environment / OWTTE / incomplete combustion (of methanol) / water forms as \({\text{ }}{{\text{H}}_2}{\text{O(l)}}\) instead of \({{\text{H}}_2}{\text{O(g)}}\);
Do not allow just “heat lost”.
Examiners report
Many errors were seen in part (a). Candidates used the wrong values from the Data Booklet, wrong coefficients were used and not all the correct bonds were selected. Some candidates also reversed the final calculation to get an endothermic enthalpy rather than an exothermic enthalpy or made careless arithmetic errors.
Candidates were proficient at correctly calculating the number of mole methanol burnt.
Candidates did not use the expression \(q = mc\Delta T\) well.
Again numerous errors were seen here with candidates using the mass of methanol rather than water, adding 273 to the temperature change calculated and not converting J to kJ. Some candidates did not recognise that the combustion of methanol is exothermic and hence did not include the negative sign for the enthalpy change.
Part (c) was generally well done, however candidates often just stated that ‘heat was lost’ in part (ii). A more detail response was expected, e.g. heat was lost to surroundings.
Part (c) was generally well done, however candidates often just stated that ‘heat was lost’ in part (ii). A more detail response was expected, e.g. heat was lost to surroundings.
Question
Ethanol is used as a component in fuel for some vehicles. One fuel mixture contains 10% by mass of ethanol in unleaded petrol (gasoline). This mixture is often referred to as Gasohol E10.
Assume that the other 90% by mass of Gasohol E10 is octane. 1.00 kg of this fuel mixture was burned.
\[\begin{array}{*{20}{l}} {{\text{C}}{{\text{H}}_3}{\text{C}}{{\text{H}}_2}{\text{OH(l)}} + {\text{3}}{{\text{O}}_2}{\text{(g)}} \to {\text{2C}}{{\text{O}}_2}{\text{(g)}} + {\text{3}}{{\text{H}}_2}{\text{O(l)}}}&{\Delta {H^\Theta } = – 1367{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}} \\ {{{\text{C}}_8}{{\text{H}}_{18}}{\text{(l)}} + {\text{12}}\frac{1}{2}{{\text{O}}_2}{\text{(g)}} \to {\text{8C}}{{\text{O}}_2}{\text{(g)}} + {\text{9}}{{\text{H}}_2}{\text{O(l)}}}&{\Delta {H^\Theta } = – 5470{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}} \end{array}\]
Calculate the mass, in g, of ethanol and octane in 1.00 kg of the fuel mixture.
Calculate the amount, in mol, of ethanol and octane in 1.00 kg of the fuel mixture.
Calculate the total amount of energy, in kJ, released when 1.00 kg of the fuel mixture is completely burned.
If the fuel blend was vaporized before combustion, predict whether the amount of energy released would be greater, less or the same. Explain your answer.
Answer/Explanation
Markscheme
(10% 1000 g =) 100 g ethanol and (90% 1000 g =) 900 g octane;
\(n{\text{(ethanol)}} = 2.17{\text{ mol}}\) and \(n{\text{(octane)}} = 7.88{\text{ mol}}\);
\({{\text{E}}_{{\text{released from ethanol}}}} = (2.17 \times 1367) = 2966{\text{ (kJ)}}\);
\({{\text{E}}_{{\text{released from octane}}}} = (7.88 \times 5470) = 43104{\text{ (kJ)}}\);
total energy released \( = (2966 + 43104) = 4.61 \times {10^4}{\text{ (kJ)}}\);
Award [3] for correct final answer.
Accept answers using whole numbers for molar masses and rounding.
greater;
fewer intermolecular bonds/forces to break / vaporization is endothermic / gaseous fuel has greater enthalpy than liquid fuel / OWTTE;
M2 cannot be scored if M1 is incorrect.
Examiners report
Candidates were able to calculate the mass of ethanol and octane in the fuel mixture. The most common error here involved not expressing the answer in the requested units of grams. A number of candidates expressed answers in kg.
Many candidates were able to calculate the number of mole of ethanol and octane in (a) (ii) but errors in the calculation of molar mass were seen regularly. Candidates should also use the relative atomic masses, expressed to two decimal places as in the Periodic Table provided in the Data Table.
In part (a) (iii) some candidates multiplied incorrect numbers together or did not consider the number of moles of each part of the fuel mixture. Some candidates just added the enthalpies of combustion provided in the questions.
Part (b) was found to be very challenging by candidates. Very few candidates had the depth of understanding to answer this question adequately.
