Inverse function IB Style Questions Examples And Solutions
Question 12. [Maximum mark: 21]
A function is defined by
\(f(x)=arcsin\frac{x^{2}-1}{x^{2}+1} , x\in R\)
(a) Show that is an even function.
(b) By considering limits, show that the graph of y=f(x) has a horizontal asymptote and state its equation.
(c) (i) Show that \({f}'(x)=\frac{2x}{\sqrt{x^{2}(x^{2}+1)}}\) ;
for \(x\in R\) , \(x\neq 0\)
(ii) By using the expression for f'(x) and the result \(√ x^{2} = |x|\) , show that f is decreasing for x < 0.
A function g is defined by \(f(x)=arcsin\frac{x^{2}-1}{x^{2}+1} , x\in R\) and \(x\geq 0\)
(d) Find an expression for \(g^{-1}(x)\), justifying your answer.
(e) State the domain of \(g^{-1}\).
(f) Sketch the graph of \(y= g ^{- 1} (x )\) clearly indicating any asymptotes with their equations and stating the values of any axes intercepts.
▶️Answer/Explanation
(a) \(f(-x)=arcsin(\frac{(-x^{2})-1}{(-x^{2})+1})=arcsin(\frac{(x^{2})-1}{(x^{2})+1})\)
so , \(f(-x)=f(x) \rightarrow even function\).
(b) as\( x \to \pm \infty , f(x)\rightarrow arcsin1(\rightarrow \frac{x}{2})
so the horizontal asymtote is y= \frac{\Pi }{2}\)
(e) domain is \(\frac{-\Pi}{2}\leq x\leq \frac{\Pi}{2}\)
(f)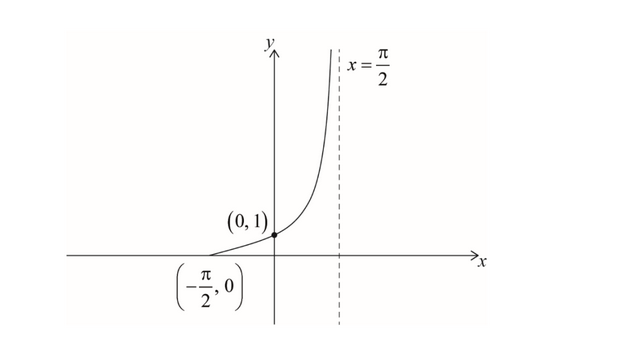 
Inverse function
A function accepts values, performs particular operations on these values and generates an output. The inverse function agrees with the resultant, operates and reaches back to the original function.
| The inverse function returns the original value for which a function gave the output. |
If you consider functions, f and g are inverse, f(g(x)) = g(f(x)) = x. A function that consists of its inverse fetches the original value.
Example: f(x) = 2x + 5 = y
Then, g(y) = (y-5)/2 = x is the inverse of f(x).
Note:
- The relation, developed when the independent variable is interchanged with the variable which is dependent on a specified equation and this inverse may or may not be a function.
- If the inverse of a function is itself, then it is known as inverse function, denoted by f-1(x).
Inverse Function Graph
The graph of the inverse of a function reflects two things, one is the function and second is the inverse of the function, over the line y = x. This line in the graph passes through the origin and has slope value 1. It can be represented as;
y = f-1(x)
which is equal to;
x = f(y)
This relation is somewhat similar to y = f(x), which defines the graph of f but the part of x and y are reversed here. So if we have to draw the graph of f-1, then we have to switch the positions of x and y in axes.
Question
A function f is defined by \(f(x)=arcsin\frac{x^2-1}{x^2+1},\;x\in \mathbb{R}\)
(a) Show that f is an even function. [1]
(b) By considering limits, show that the graph of y = f (x) has a horizontal asymptote and state its equation. [2]
(c) (i) Show that \(f{}'(x)=\frac{2x}{\sqrt{x^2}(x^2+1)} \; for\; x\in \mathbb{R},\;x\neq 0\)
(ii) By using the expression for f ′(x) and the result \(\sqrt{x^2}=\left | x \right |\) show that f is decreasing for x < 0 . [9]
A function g is defined by \(g(x)=arcsin\frac{x^2-1}{x^2+1},\;x\in \mathbb{R},\;x\geq 0.\)
(d) Find an expression for g-1(x) , justifying your answer. [5]
(e) State the domain of g-1 . [1]
(f) Sketch the graph of y = g-1(x) , clearly indicating any asymptotes with their equations and stating the values of any axes intercepts. [3]
▶️Answer/Explanation
Ans:
(a) Since $$\begin{eqnarray} f\left(-x\right) &=& \arcsin\left[\frac{\left(-x\right)^2-1}{\left(-x\right)^2+1}\right] \nonumber \\ &=& \arcsin\left(\frac{x^2-1}{x^2+1}\right) \nonumber \\ &=& f\left(x\right), \nonumber \\ \end{eqnarray}$$ $f$ is an even function.
(b) Consider $\lim_{x\to\infty} \arcsin\left(\frac{x^2-1}{x^2+1}\right)$, we have $$\begin{eqnarray} \lim_{x\to\infty} \arcsin\left(\frac{x^2-1}{x^2+1}\right) &=& \lim_{x\to\infty} \arcsin\left(\frac{1-\frac{1}{x^2}}{1+\frac{1}{x^2}}\right) \nonumber \\ &=& \arcsin\left(1\right) \nonumber \\ &=& \frac{\pi}{2}, \end{eqnarray}$$ i.e., $y=\frac{\pi}{2}$ is a horizontal asymptote.
(c)(i) Taking sine on both sides of $\arcsin\left(\frac{x^2-1}{x^2+1}\right)$, we have $\sin\left[f\left(x\right)\right]=\frac{x^2-1}{x^2+1}$.
Differentiating both sides with respect to $x$, we have $$\begin{eqnarray} f’\left(x\right)\cos\left[f\left(x\right)\right]=\frac{2x\left(x^2+1\right)-2x\left(x^2-1\right)}{\left(x^2+1\right)^2}. \end{eqnarray}$$ Rearranging, we have $$\begin{eqnarray} f’\left(x\right) &=& \frac{4x}{\left(x^2+1\right)^2}\times\frac{1}{\cos\left[f\left(x\right)\right]} \nonumber \\ &=& \frac{4x}{\left(x^2+1\right)^2}\times\frac{x^2+1}{2\sqrt{x^2}} \nonumber \\ &=& \frac{2x}{\sqrt{x^2}\left(x^2+1\right)}, \end{eqnarray}$$ since by Pythagoras’ Theorem, we can find $\cos\left[f\left(x\right)\right]=\frac{2\sqrt{x^2}}{x^2+1}$.
(c)(ii) When $x\lt 0$, $\sqrt{x^2}=\left|x\right|\gt 0$ and $x^2+1\gt 0$. Thus, $$\begin{eqnarray} \frac{2x}{\sqrt{x^2}\left(x^2+1\right)} \lt 0, \end{eqnarray}$$ i.e., $f$ is decreasing for $x\lt 0$.
(d) Let $y=\arcsin\left(\frac{x^2-1}{x^2+1}\right)$, then making $x$ the subject, we have $$\begin{eqnarray} \sin y=\frac{x^2-1}{x^2+1} \nonumber \\ \sin y\left(x^2+1\right) = x^2-1 \nonumber \\ x^2\left(\sin y-1\right) = -1-\sin y \nonumber \\ x^2 = \frac{1+\sin y}{1-\sin y} \nonumber \\ x = \pm\sqrt{\frac{1+\sin y}{1-\sin y}}. \end{eqnarray}$$ Since $x\geq 0$, $g^{-1}\left(x\right)=\sqrt{\frac{1+\sin x}{1-\sin x}}$.
(e) $\text{D}_{g^{-1}}=\text{R}_g=\left[-\frac{\pi}{2},\frac{\pi}{2}\right)$.
(f) (graph to be added in later)
Question
Consider the function \(g\) , where \(g(x) = \frac{{3x}}{{5 + {x^2}}}\) .
(a) Given that the domain of \(g\) is \(x \geqslant a\) , find the least value of \(a\) such that \(g\) has an inverse function.
(b) On the same set of axes, sketch
(i) the graph of \(g\) for this value of \(a\) ;
(ii) the corresponding inverse, \({g^{ – 1}}\) .
(c) Find an expression for \({g^{ – 1}}(x)\) .
▶️Answer/Explanation
Markscheme
(a) \(a = 2.24\) \(\sqrt 5 \) A1
(b) (i)
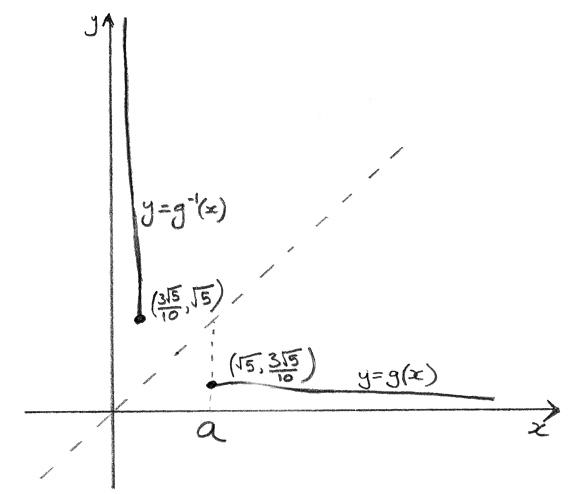A2
Note: Award A1 for end point
A1 for its asymptote.
(ii) sketch of \({g^{ – 1}}\) (see above) A2
Note: Award A1 for end point
A1 for its asymptote.
(c) \(y = \frac{{3x}}{{5 + {x^2}}} \Rightarrow y{x^2} – 3x + 5y = 0\) M1
\( \Rightarrow x = \frac{{3 \pm \sqrt {9 – 20{y^2}} }}{{2y}}\) A1
\({g^{ – 1}}(x) = \frac{{3 \pm \sqrt {9 – 20{x^2}} }}{{2x}}\) A1
[8 marks]
Examiners report
Very few completely correct answers were given to this question. Many students found a to be \(0\) and many failed to provide adequate sketches. There were very few correct answers to part (c) although many students were able to obtain partial marks.
Question
The function f is defined as \(f(x) = – 3 + \frac{1}{{x – 2}},{\text{ }}x \ne 2\).
a.(i) Sketch the graph of \(y = f(x)\), clearly indicating any asymptotes and axes intercepts.
(ii) Write down the equations of any asymptotes and the coordinates of any axes intercepts.[4]
▶️Answer/Explanation
Markscheme
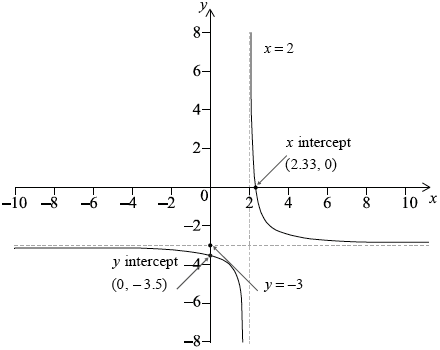A1A1A1
Note: Award A1 for correct shape, A1 for \(x = 2\) clearly stated and A1 for \(y = – 3\) clearly stated.
x intercept (2.33, 0) and y intercept (0, –3.5) A1
Note: Accept –3.5 and 2.33 (7/3) marked on the correct axes.
[4 marks]
\(x = – 3 + \frac{1}{{y – 2}}\) M1
Note: Award M1 for interchanging x and y (can be done at a later stage).
\(x + 3 = \frac{1}{{y – 2}}\)
\(y – 2 = \frac{1}{{x + 3}}\) M1
Note: Award M1 for attempting to make y the subject.
\({f^{ – 1}}(x) = 2 + \frac{1}{{x + 3}}\left( { = \frac{{2x + 7}}{{x + 3}}} \right),{\text{ }}x \ne – 3\) A1A1
Note: Award A1 only if \({f^{ – 1}}(x)\) is seen. Award A1 for the domain.
[4 marks]