Question
(a) Sketch the curve \(y = \left| {\ln x} \right| – \left| {\cos x} \right| – 0.1\) , \(0 < x < 4\) showing clearly the coordinates of the points of intersection with the x-axis and the coordinates of any local maxima and minima.
(b) Find the values of x for which \(\left| {\ln x} \right| > \left| {\cos x} \right| + 0.1\), \(0 < x < 4\) .
▶️Answer/Explanation
Markscheme
(a)
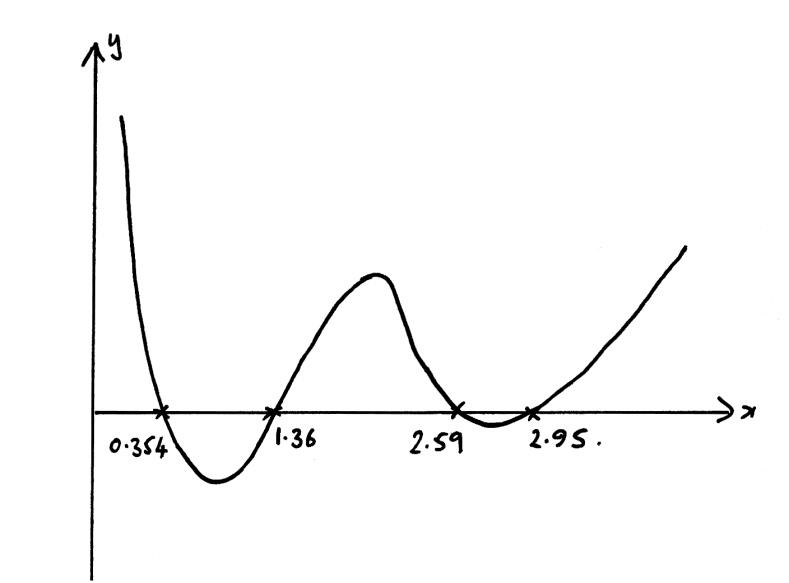 A1
A1
Note: Award A1 for shape.
x-intercepts 0.354, 1.36, 2.59, 2.95 A2
Note: Award A1 for three correct, A0 otherwise.
maximum = (1.57, 0.352) = \(\left( {\frac{\pi }{2},0.352} \right)\) A1
minimum = (1, – 0.640) and (2.77, – 0.0129) A1
(b) \(0 < x < 0.354,{\text{ }}1.36 < x < 2.59,{\text{ }}2.95 < x < 4\) A2
Note: Award A1 if two correct regions given.
[7 marks]
Examiners report
Solutions to this question were extremely disappointing with many candidates doing the sketch in degree mode instead of radian mode. The two adjacent intercepts at 2.59 and 2.95 were often missed due to an unsatisfactory window. Some sketches were so small that a magnifying glass was required to read some of the numbers; candidates would be well advised to draw sketches large enough to be easily read.
Question
Consider the functions \(f(x) = {x^3} + 1\) and \(g(x) = \frac{1}{{{x^3} + 1}}\). The graphs of \(y = f(x)\) and \(y = g(x)\) meet at the point (0, 1) and one other point, P.
a.Find the coordinates of P.[1]
b.Calculate the size of the acute angle between the tangents to the two graphs at the point P.[4]
▶️Answer/Explanation
Markscheme
\({x^3} + 1 = \frac{1}{{{x^3} + 1}}\)
\(( – 1.26, – 1)\,\,\,\,\,\left( { = \left( { – \sqrt[3]{2}, – 1} \right)} \right)\) A1
[1 mark]
\(f'( – 1.259…) = 4.762…\) \((3 \times {2^{\frac{2}{3}}})\) A1
\(g'( – 1.259…) = – 4.762…\) \(( – 3 \times {2^{\frac{2}{3}}})\) A1
required angle \( = 2\arctan \left( {\frac{1}{{4.762…}}} \right)\) M1
\( = 0.414\) (accept 23.7 ) A1
Note: Accept alternative methods including finding the obtuse angle first.
[4 marks]
Examiners report
In part (a) almost all candidates obtained the correct answer, either in numerical form or in exact form. Although many candidates scored one mark in (b), for one gradient, few scored any more. Successful candidates almost always adopted a vector approach to finding the angle between the two tangents, rather than using trigonometry.
In part (a) almost all candidates obtained the correct answer, either in numerical form or in exact form. Although many candidates scored one mark in (b), for one gradient, few scored any more. Successful candidates almost always adopted a vector approach to finding the angle between the two tangents, rather than using trigonometry.
Question
The function \(f(x) = 3\sin x + 4\cos x\) is defined for \(0 < x < 2\pi \) .
a.Write down the coordinates of the minimum point on the graph of f .[1]
b.The points \({\text{P}}(p,{\text{ }}3)\) and \({\text{Q}}(q,{\text{ }}3){\text{, }}q > p\), lie on the graph of \(y = f(x)\) .
Find p and q .[2]
c.Find the coordinates of the point, on \(y = f(x)\) , where the gradient of the graph is 3.[4]
d.Find the coordinates of the point of intersection of the normals to the graph at the points P and Q.[7]
▶️Answer/Explanation
Markscheme
\((3.79, – 5)\) A1
[1 mark]
\(p = 1.57{\text{ or }}\frac{\pi }{2},{\text{ }}q = 6.00\) A1A1
[2 marks]
\(f'(x) = 3\cos x – 4\sin x\) (M1)(A1)
\(3\cos x – 4\sin x = 3 \Rightarrow x = 4.43…\) (A1)
\((y = -4)\) A1
Coordinates are \((4.43, -4)\)
[4 marks]
\({m_{{\text{normal}}}} = \frac{1}{{{m_{{\text{tangent}}}}}}\) (M1)
gradient at P is \( – 4\) so gradient of normal at P is \(\frac{1}{4}\) (A1)
gradient at Q is 4 so gradient of normal at Q is \( – \frac{1}{4}\) (A1)
equation of normal at P is \(y – 3 = \frac{1}{4}(x – 1.570…){\text{ }}({\text{or }}y = 0.25x + 2.60…)\) (M1)
equation of normal at Q is \(y – 3 = \frac{1}{4}(x – 5.999…){\text{ }}({\text{or }}y = -0.25x + \underbrace {4.499…}_{})\) (M1)
Note: Award the previous two M1 even if the gradients are incorrect in \(y – b = m(x – a)\) where \((a,b)\) are coordinates of P and Q (or in \(y = mx + c\) with c determined using coordinates of P and Q.
intersect at \((3.79,{\text{ }}3.55)\) A1A1
Note: Award N2 for 3.79 without other working.
[7 marks]
Question
a.Find \(\int {x{{\sec }^2}x{\text{d}}x} \).[4]
b.Determine the value of m if \(\int_0^m {x{{\sec }^2}x{\text{d}}x = 0.5} \), where m > 0.[2]
▶️Answer/Explanation
Markscheme
\(\int {x{{\sec }^2}x{\text{d}}x} = x\tan x – \int {1 \times \tan x{\text{d}}x} \) M1A1
\( = x\tan x + \ln \left| {\cos x} \right|( + c){\text{ }}\left( { = x\tan x – \ln \left| {\sec x} \right|( + c)} \right)\) M1A1
[4 marks]
attempting to solve an appropriate equation eg \(m\tan m + \ln (\cos m) = 0.5\) (M1)
m = 0.822 A1
Note: Award A1 if m = 0.822 is specified with other positive solutions.
[2 marks]
Examiners report
In part (a), a large number of candidates were able to use integration by parts correctly but were unable to use integration by substitution to then find the indefinite integral of tan x. In part (b), a large number of candidates attempted to solve the equation without direct use of a GDC’s numerical solve command. Some candidates stated more than one solution for m and some specified m correct to two significant figures only.
In part (a), a large number of candidates were able to use integration by parts correctly but were unable to use integration by substitution to then find the indefinite integral of tan x. In part (b), a large number of candidates attempted to solve the equation without direct use of a GDC’s numerical solve command. Some candidates stated more than one solution for m and some specified m correct to two significant figures only.
