Question
A particle P moves in a straight line with displacement relative to origin given by
\[s = 2\sin (\pi t) + \sin (2\pi t),{\text{ }}t \geqslant 0,\]
where t is the time in seconds and the displacement is measured in centimetres.
(i) Write down the period of the function s.
(ii) Find expressions for the velocity, v, and the acceleration, a, of P.
(iii) Determine all the solutions of the equation v = 0 for \(0 \leqslant t \leqslant 4\).
Consider the function
\[f(x) = A\sin (ax) + B\sin (bx),{\text{ }}A,{\text{ }}a,{\text{ }}B,{\text{ }}b,{\text{ }}x \in \mathbb{R}.\]
Use mathematical induction to prove that the\({(2n)^{{\text{th}}}}\) derivative of f is given by \(({f^{(2n)}}(x) = {( – 1)^n}\left( {A{a^{2n}}\sin (ax) + B{b^{2n}}\sin (bx)} \right)\), for all \(n \in {\mathbb{Z}^ + }\).
Answer/Explanation
Markscheme
(i) the period is 2 A1
(ii) \(v = \frac{{{\text{d}}s}}{{{\text{d}}t}} = 2\pi \cos (\pi t) + 2\pi \cos (2\pi t)\) (M1)A1
\(a = \frac{{{\text{d}}v}}{{{\text{d}}t}} = – 2{\pi ^2}\sin (\pi t) – 4{\pi ^2}\sin (2\pi t)\) (M1)A1
(iii) \(v = 0\)
\(2\pi \left( {\cos (\pi t) + \cos (2\pi t)} \right) = 0\)
EITHER
\(\cos (\pi t) + 2{\cos ^2}(\pi t) – 1 = 0\) M1
\(\left( {2\cos (\pi t) – 1} \right)\left( {\cos (\pi t) + 1} \right) = 0\) (A1)
\(\cos (\pi t) = \frac{1}{2}{\text{ or }}\cos (\pi t) = – 1\) A1
\(t = \frac{1}{3},{\text{ }}t = 1\) A1
\(t = \frac{5}{3},{\text{ }}t = \frac{7}{3},{\text{ }}t = \frac{{11}}{3},{\text{ }}t = 3\) A1
OR
\(2\cos \left( {\frac{{\pi t}}{2}} \right)\cos \left( {\frac{{3\pi t}}{2}} \right) = 0\) M1
\(\cos \left( {\frac{{\pi t}}{2}} \right) = 0{\text{ or }}\cos \left( {\frac{{3\pi t}}{2}} \right) = 0\) A1A1
\(t = \frac{1}{3},{\text{ 1}}\) A1
\(t = \frac{5}{3},{\text{ }}\frac{7}{3},{\text{ }}3,{\text{ }}\frac{{11}}{3}\) A1
[10 marks]
\(P(n):{f^{(2n)}}(x) = {( – 1)^n}\left( {A{a^{2n}}\sin (ax) + B{b^{2n}}\sin (bx)} \right)\)
\(P(1):f”(x) = {\left( {Aa\cos (ax) + Bb\cos (bx)} \right)^\prime }\) M1
\( = – A{a^2}\sin (ax) – B{b^2}\sin (bx)\)
\( = – 1\left( {A{a^2}\sin (ax) + B{b^2}\sin (bx)} \right)\) A1
\(\therefore P(1)\) true
assume that
\(P(k):{f^{(2k)}}(x) = {( – 1)^k}\left( {A{a^{2k}}\sin (ax) + B{b^{2k}}\sin (bx)} \right)\) is true M1
consider \(P(k + 1)\)
\({f^{(2k + 1)}}(x) = {( – 1)^k}\left( {A{a^{2k + 1}}\cos (ax) + B{b^{2k + 1}}\cos (bx)} \right)\) M1A1
\({f^{(2k + 2)}}(x) = {( – 1)^k}\left( { – A{a^{2k + 2}}\sin (ax) – B{b^{2k + 2}}\sin (bx)} \right)\) A1
\( = {( – 1)^{k + 1}}\left( {A{a^{2k + 2}}\sin (ax) + B{b^{2k + 2}}\sin (bx)} \right)\) A1
\(P(k)\) true implies \(P(k + 1)\) true, \(P(1)\) true so \(P(n)\) true \(\forall n \in {\mathbb{Z}^ + }\) R1
Note: Award the final R1 only if the previous three M marks have been awarded.
[8 marks]
Examiners report
In (a), only a few candidates gave the correct period but the expressions for velocity and acceleration were correctly obtained by most candidates. In (a)(iii), many candidates manipulated the equation v = 0 correctly to give the two possible values for \(\cos (\pi t)\) but then failed to find all the possible values of t.
Solutions to (b) were disappointing in general with few candidates giving a correct solution.
Question
Given that \(y = \frac{1}{{1 – x}}\), use mathematical induction to prove that \(\frac{{{{\text{d}}^n}y}}{{{\text{d}}{x^n}}} = \frac{{n!}}{{{{(1 – x)}^{n + 1}}}},{\text{ }}n \in {\mathbb{Z}^ + }\).
Answer/Explanation
Markscheme
proposition is true for n = 1 since \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{1}{{{{(1 – x)}^2}}}\) M1
\( = \frac{{1!}}{{{{(1 – x)}^2}}}\) A1
Note: Must see the 1! for the A1.
assume true for n = k, \(k \in {\mathbb{Z}^ + }\), i.e. \(\frac{{{{\text{d}}^k}y}}{{{\text{d}}{x^k}}} = \frac{{k!}}{{{{(1 – x)}^{k + 1}}}}\) M1
consider \(\frac{{{{\text{d}}^{k + 1}}y}}{{{\text{d}}{x^{k + 1}}}} = \frac{{{\text{d}}\left( {\frac{{{{\text{d}}^k}y}}{{{\text{d}}{x^k}}}} \right)}}{{{\text{d}}x}}\) (M1)
\( = (k + 1)k!{(1 – x)^{ – (k + 1) – 1}}\) A1
\( = \frac{{(k + 1)!}}{{{{(1 – x)}^{k + 2}}}}\) A1
hence, \({{\text{P}}_{k + 1}}\) is true whenever \({{\text{P}}_{k}}\) is true, and \({{\text{P}}_1}\) is true, and therefore the proposition is true for all positive integers R1
Note: The final R1 is only available if at least 4 of the previous marks have been awarded.
[7 marks]
Examiners report
Most candidates were awarded good marks for this question. A disappointing minority thought that the \((k + 1)\)th derivative was the \((k)\)th derivative multiplied by the first derivative. Providing an acceptable final statement remains a perennial issue.
Question
Show that \(\sin \left( {\theta + \frac{\pi }{2}} \right) = \cos \theta \).
Consider \(f(x) = \sin (ax)\) where \(a\) is a constant. Prove by mathematical induction that \({f^{(n)}}(x) = {a^n}\sin \left( {ax + \frac{{n\pi }}{2}} \right)\) where \(n \in {\mathbb{Z}^ + }\) and \({f^{(n)}}(x)\) represents the \({{\text{n}}^{{\text{th}}}}\) derivative of \(f(x)\).
Answer/Explanation
Markscheme
\(\sin \left( {\theta + \frac{\pi }{2}} \right) = \sin \theta \cos \frac{\pi }{2} + \cos \theta \sin \frac{\pi }{2}\) M1
\( = \cos \theta \) AG
Note: Accept a transformation/graphical based approach.
[1 mark]
consider \(n = 1,{\text{ }}f'(x) = a\cos (ax)\) M1
since \(\sin \left( {ax + \frac{\pi }{2}} \right) = \cos ax\) then the proposition is true for \(n = 1\) R1
assume that the proposition is true for \(n = k\) so \({f^{(k)}}(x) = {a^k}\sin \left( {ax + \frac{{k\pi }}{2}} \right)\) M1
\({f^{(k + 1)}}(x) = \frac{{{\text{d}}\left( {{f^{(k)}}(x)} \right)}}{{{\text{d}}x}}\;\;\;\left( { = a\left( {{a^k}\cos \left( {ax + \frac{{k\pi }}{2}} \right)} \right)} \right)\) M1
\( = {a^{k + 1}}\sin \left( {ax + \frac{{k\pi }}{2} + \frac{\pi }{2}} \right)\) (using part (a)) A1
\( = {a^{k + 1}}\sin \left( {ax + \frac{{(k + 1)\pi }}{2}} \right)\) A1
given that the proposition is true for \(n = k\) then we have shown that the proposition is true for \(n = k + 1\). Since we have shown that the proposition is true for \(n = 1\) then the proposition is true for all \(n \in {\mathbb{Z}^ + }\) R1
Note: Award final R1 only if all prior M and R marks have been awarded.
[7 marks]
Total [8 marks]
Examiners report
[N/A]
[N/A]
Question
The following graph shows the relation \(x = 3\cos 2y + 4,{\text{ }}0 \leqslant y \leqslant \pi \).
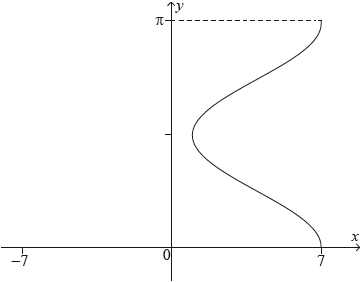
The curve is rotated 360° about the \(y\)-axis to form a volume of revolution.
A container with this shape is made with a solid base of diameter 14 cm . The container is filled with water at a rate of \({\text{2 c}}{{\text{m}}^{\text{3}}}\,{\text{mi}}{{\text{n}}^{ – 1}}\). At time \(t\) minutes, the water depth is \(h{\text{ cm, }}0 \leqslant h \leqslant \pi \) and the volume of water in the container is \(V{\text{ c}}{{\text{m}}^{\text{3}}}\).
Calculate the value of the volume generated.
(i) Given that \(\frac{{{\text{d}}V}}{{{\text{d}}h}} = \pi {(3\cos 2h + 4)^2}\), find an expression for \(\frac{{{\text{d}}h}}{{{\text{d}}t}}\).
(ii) Find the value of \(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) when \(h = \frac{\pi }{4}\).
(i) Find \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}}\).
(ii) Find the values of \(h\) for which \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}} = 0\).
(iii) By making specific reference to the shape of the container, interpret \(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) at the values of \(h\) found in part (c)(ii).
Answer/Explanation
Markscheme
use of \(\pi \int_a^b {{x^2}{\text{d}}y} \) (M1)
Note: Condone any or missing limits.
\(V = \pi \int_0^\pi {{{(3\cos 2y + 4)}^2}{\text{d}}y} \) (A1)
\( = \pi \int_0^\pi {(9{{\cos }^2}2y + 24\cos 2y + 16){\text{d}}y} \) A1
\(9{\cos ^2}2y = \frac{9}{2}(1 + \cos 4y)\) (M1)
\( = \pi \left[ {\frac{{9y}}{2} + \frac{9}{8}\sin 4y + 12\sin 2y + 16y} \right]_0^\pi \) M1A1
\( = \pi \left( {\frac{{9\pi }}{2} + 16\pi } \right)\) (A1)
\( = \frac{{41{\pi ^2}}}{2}{\text{ (c}}{{\text{m}}^3})\) A1
Note: If the coefficient “\(\pi \)” is absent, or eg, “\(2\pi \)” is used, only M marks are available.
[8 marks]
(i) attempting to use \(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{{{\text{d}}V}}{{{\text{d}}t}} \times \frac{{{\text{d}}h}}{{{\text{d}}V}}\) with \(\frac{{{\text{d}}V}}{{{\text{d}}t}} = 2\) M1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{2}{{\pi {{(3\cos 2h + 4)}^2}}}\) A1
(ii) substituting \(h = \frac{\pi }{4}\) into \(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) (M1)
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{1}{{8\pi }}{\text{ (cm}}\,{\text{mi}}{{\text{n}}^{ – 1}})\) A1
Note: Do not allow FT marks for (b)(ii).
[4 marks]
(i) \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}} = \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{{{\text{d}}h}}{{{\text{d}}t}}} \right) = \frac{{{\text{d}}h}}{{{\text{d}}t}} \times \frac{{\text{d}}}{{{\text{d}}h}}\left( {\frac{{{\text{d}}h}}{{{\text{d}}t}}} \right)\) (M1)
\( = \frac{2}{{\pi {{(3\cos 2h + 4)}^2}}} \times \frac{{24\sin 2h}}{{\pi {{(3\cos 2h + 4)}^3}}}\) M1A1
Note: Award M1 for attempting to find \(\frac{{\text{d}}}{{{\text{d}}h}}\left( {\frac{{{\text{d}}h}}{{{\text{d}}t}}} \right)\).
\( = \frac{{48\sin 2h}}{{{\pi ^2}{{(3\cos 2h + 4)}^5}}}\) A1
(ii) \(\sin 2h = 0 \Rightarrow h = 0,{\text{ }}\frac{\pi }{2},{\text{ }}\pi \) A1
Note: Award A1 for \(\sin 2h = 0 \Rightarrow h = 0,{\text{ }}\frac{\pi }{2},{\text{ }}\pi \) from an incorrect \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}}\).
(iii) METHOD 1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) is a minimum at \(h = 0,{\text{ }}\pi \) and the container is widest at these values R1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) is a maximum at \(h = \frac{\pi }{2}\) and the container is narrowest at this value R1
[7 marks]
Examiners report
Part (a) was often answered well, though for some reason a minority tended to use the incorrect \(\pi \int {{{(3\cos 2y)}^2}{\text{d}}y} \) and gained few marks thereafter. Incorrect limits were sometimes seen, which led to only method marks being available. A pleasing number were able to deal with the integration of \({\cos ^2}2y\) through the use of the correct identity.
Part (b) was well answered and did not pose too many problems.
Correct answers to part (c) were rarely seen. Only the very best candidates appreciated the correct use of the chain rule when trying to determine an expression for \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}}\).
Question
Let \(y = {{\text{e}}^x}\sin x\).
Consider the function \(f\) defined by \(f(x) = {{\text{e}}^x}\sin x,{\text{ }}0 \leqslant x \leqslant \pi \).
The curvature at any point \((x,{\text{ }}y)\) on a graph is defined as \(\kappa = \frac{{\left| {\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}}} \right|}}{{{{\left( {1 + {{\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)}^2}} \right)}^{\frac{3}{2}}}}}\).
Find an expression for \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).
Show that \(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2{{\text{e}}^x}\cos x\).
Show that the function \(f\) has a local maximum value when \(x = \frac{{3\pi }}{4}\).
Find the \(x\)-coordinate of the point of inflexion of the graph of \(f\).
Sketch the graph of \(f\), clearly indicating the position of the local maximum point, the point of inflexion and the axes intercepts.
Find the area of the region enclosed by the graph of \(f\) and the \(x\)-axis.
The curvature at any point \((x,{\text{ }}y)\) on a graph is defined as \(\kappa = \frac{{\left| {\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}}} \right|}}{{{{\left( {1 + {{\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)}^2}} \right)}^{\frac{3}{2}}}}}\).
Find the value of the curvature of the graph of \(f\) at the local maximum point.
Find the value \(\kappa \) for \(x = \frac{\pi }{2}\) and comment on its meaning with respect to the shape of the graph.
Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {{\text{e}}^x}\sin x + {{\text{e}}^x}\cos x{\text{ }}\left( { = {{\text{e}}^x}(\sin x + \cos x)} \right)\) M1A1
[2 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = {{\text{e}}^x}(\sin x + \cos x) + {{\text{e}}^x}(\cos x – \sin x)\) M1A1
\( = 2{{\text{e}}^x}\cos x\) AG
[2 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {{\text{e}}^{\frac{{3\pi }}{4}}}\left( {\sin \frac{{3\pi }}{4} + \cos \frac{{3\pi }}{4}} \right) = 0\) R1
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2{{\text{e}}^{\frac{{3\pi }}{4}}}\cos \frac{{3\pi }}{4} < 0\) R1
hence maximum at \(x = \frac{{3\pi }}{4}\) AG
[2 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 0 \Rightarrow 2{{\text{e}}^x}\cos x = 0\) M1
\( \Rightarrow x = \frac{\pi }{2}\) A1
Note: Award M1A0 if extra zeros are seen.
[2 marks]
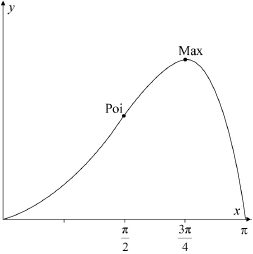
correct shape and correct domain A1
max at \(x = \frac{{3\pi }}{4}\), point of inflexion at \(x = \frac{\pi }{2}\) A1
zeros at \(x = 0\) and \(x = \pi \) A1
Note: Penalize incorrect domain with first A mark; allow FT from (d) on extra points of inflexion.
[3 marks]
EITHER
\(\int_0^x {{{\text{e}}^x}\sin x{\text{d}}x = [{{\text{e}}^x}\sin x]_0^\pi – \int_0^\pi {{{\text{e}}^x}\cos x{\text{d}}x} } \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [{{\text{e}}^x}\sin x]_0^\pi – \left( {[{{\text{e}}^x}\cos x]_0^x + \int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x} } \right)} \) A1
OR
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [ – {{\text{e}}^x}\cos x]_0^\pi + \int_0^\pi {{{\text{e}}^x}\cos x{\text{d}}x} } \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [ – {{\text{e}}^x}\cos x]} _0^\pi + \left( {[{{\text{e}}^x}\sin x]_0^\pi – \int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x} } \right)\) A1
THEN
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = \frac{1}{2}\left( {[{{\text{e}}^x}\sin x]_0^x – [{{\text{e}}^x}\cos x]_0^x} \right)} \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = \frac{1}{2}({{\text{e}}^x} + 1)} \) A1
[6 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) (A1)
\(\frac{{{d^2}y}}{{d{x^2}}} = 2{e^{\frac{{3\pi }}{4}}}\cos \frac{{3\pi }}{4} = – \sqrt 2 {e^{\frac{{3\pi }}{4}}}\) (A1)
\(\kappa = \frac{{\left| { – \sqrt 2 {{\text{e}}^{\frac{{3\pi }}{4}}}} \right|}}{1} = \sqrt 2 {{\text{e}}^{\frac{{3\pi }}{4}}}\) A1
[3 marks]
\(\kappa = 0\) A1
the graph is approximated by a straight line R1
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
Let \(f(x) = \cos x\).
Let \(g(x) = {x^k}\), where \(k \in {\mathbb{Z}^ + }\).
Let \(k = 21\) and \(h(x) = \left( {{f^{(19)}}(x) \times {g^{(19)}}(x)} \right)\).
(i) Find the first four derivatives of \(f(x)\).
(ii) Find \({f^{(19)}}(x)\).
(i) Find the first three derivatives of \(g(x)\).
(ii) Given that \({g^{(19)}}(x) = \frac{{k!}}{{(k – p)!}}({x^{k – 19}})\), find \(p\).
(i) Find \(h'(x)\).
(ii) Hence, show that \(h'(\pi ) = \frac{{ – 21!}}{2}{\pi ^2}\).
Answer/Explanation
Markscheme
(i) \(f'(x) = – \sin x,{\text{ }}f”(x) = – \cos x,{\text{ }}{f^{(3)}}(x) = \sin x,{\text{ }}{f^{(4)}}(x) = \cos x\) A2 N2
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)recognizing that 19 is one less than a multiple of 4, \({f^{(19)}}(x) = {f^{(3)}}(x)\)
\({f^{(19)}}(x) = \sin x\) A1 N2
[4 marks]
(i) \(g'(x) = k{x^{k – 1}}\)
\(g”(x) = k(k – 1){x^{k – 2}},{\text{ }}{g^{(3)}}(x) = k(k – 1)(k – 2){x^{k – 3}}\) A1A1 N2
(ii) METHOD 1
correct working that leads to the correct answer, involving the correct expression for the 19th derivative A2
eg\(\,\,\,\,\,\)\(k(k – 1)(k – 2) \ldots (k – 18) \times \frac{{(k – 19)!}}{{(k – 19)!}},{{\text{ }}_k}{P_{19}}\)
\(p = 19\) (accept \(\frac{{k!}}{{(k – 19)!}}{x^{k – 19}}\)) A1 N1
METHOD 2
correct working involving recognizing patterns in coefficients of first three derivatives (may be seen in part (b)(i)) leading to a general rule for 19th coefficient A2
eg\(\,\,\,\,\,\)\(g” = 2!\left( {\begin{array}{*{20}{c}} k \\ 2 \end{array}} \right),{\text{ }}k(k – 1)(k – 2) = \frac{{k!}}{{(k – 3)!}},{\text{ }}{g^{(3)}}(x){ = _k}{P_3}({x^{k – 3}})\)
\({g^{(19)}}(x) = 19!\left( {\begin{array}{*{20}{c}} k \\ {19} \end{array}} \right),{\text{ }}19! \times \frac{{k!}}{{(k – 19)! \times 19!}},{{\text{ }}_k}{P_{19}}\)
\(p = 19\) (accept \(\frac{{k!}}{{(k – 19)!}}{x^{k – 19}}\)) A1 N1
[5 marks]
(i) valid approach using product rule (M1)
eg\(\,\,\,\,\,\)\(uv’ + vu’,{\text{ }}{f^{(19)}}{g^{(20)}} + {f^{(20)}}{g^{(19)}}\)
correct 20th derivatives (must be seen in product rule) (A1)(A1)
eg\(\,\,\,\,\,\)\({g^{(20)}}(x) = \frac{{21!}}{{(21 – 20)!}}x,{\text{ }}{f^{(20)}}(x) = \cos x\)
\(h'(x) = \sin x(21!x) + \cos x\left( {\frac{{21!}}{2}{x^2}} \right){\text{ }}\left( {{\text{accept }}\sin x\left( {\frac{{21!}}{{1!}}x} \right) + \cos x\left( {\frac{{21!}}{{2!}}{x^2}} \right)} \right)\) A1 N3
(ii) substituting \(x = \pi \) (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\({f^{(19)}}(\pi ){g^{(20)}}(\pi ) + {f^{(20)}}(\pi ){g^{(19)}}(\pi ),{\text{ }}\sin \pi \frac{{21!}}{{1!}}\pi + \cos \pi \frac{{21!}}{{2!}}{\pi ^2}\)
evidence of one correct value for \(\sin \pi \) or \(\cos \pi \) (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\(\sin \pi = 0,{\text{ }}\cos \pi = – 1\)
evidence of correct values substituted into \(h'(\pi )\) A1
eg\(\,\,\,\,\,\)\(21!(\pi )\left( {0 – \frac{\pi }{{2!}}} \right),{\text{ }}21!(\pi )\left( { – \frac{\pi }{2}} \right),{\text{ }}0 + ( – 1)\frac{{21!}}{2}{\pi ^2}\)
Note: If candidates write only the first line followed by the answer, award A1A0A0.
\(\frac{{ – 21!}}{2}{\pi ^2}\) AG N0
[7 marks]
Question
A function f (x) has derivative f ′(x) = 3x2 + 18x. The graph of f has an x-intercept at x = −1.
Find f (x).
The graph of f has a point of inflexion at x = p. Find p.
Find the values of x for which the graph of f is concave-down.
Answer/Explanation
Markscheme
evidence of integration (M1)
eg \(\int {f’\left( x \right)} \)
correct integration (accept absence of C) (A1)(A1)
eg \({x^3} + \frac{{18}}{2}{x^2} + C,\,\,{x^3} + 9{x^2}\)
attempt to substitute x = −1 into their f = 0 (must have C) M1
eg \({\left( { – 1} \right)^3} + 9{\left( { – 1} \right)^2} + C = 0,\,\, – 1 + 9 + C = 0\)
Note: Award M0 if they substitute into original or differentiated function.
correct working (A1)
eg \(8 + C = 0,\,\,\,C = – 8\)
\(f\left( x \right) = {x^3} + 9{x^2} – 8\) A1 N5
[6 marks]
METHOD 1 (using 2nd derivative)
recognizing that f” = 0 (seen anywhere) M1
correct expression for f” (A1)
eg 6x + 18, 6p + 18
correct working (A1)
6p + 18 = 0
p = −3 A1 N3
METHOD 1 (using 1st derivative)
recognizing the vertex of f′ is needed (M2)
eg \( – \frac{b}{{2a}}\) (must be clear this is for f′)
correct substitution (A1)
eg \(\frac{{ – 18}}{{2 \times 3}}\)
p = −3 A1 N3
[4 marks]
valid attempt to use f” (x) to determine concavity (M1)
eg f” (x) < 0, f” (−2), f” (−4), 6x + 18 ≤ 0
correct working (A1)
eg 6x + 18 < 0, f” (−2) = 6, f” (−4) = −6
f concave down for x < −3 (do not accept x ≤ −3) A1 N2
[3 marks]
Question
Given that \(f(x) = \frac{1}{x}\) , answer the following.
Find the first four derivatives of \(f(x)\) .
Write an expression for \({f^{(n)}}(x)\) in terms of x and n .
Answer/Explanation
Markscheme
\(f'(x) = – {x^{ – 2}}\) (or \( – \frac{1}{{{x^2}}}\) ) A1 N1
\(f”(x) = 2{x^{ – 3}}\) (or \(\frac{2}{{{x^3}}}\) ) A1 N1
\(f”'(x) = – 6{x^{ – 4}}\) (or \( – \frac{6}{{{x^4}}}\) ) A1 N1
\({f^{(4)}}(x) = 24{x^{ – 5}}\) (or \(\frac{{24}}{{{x^5}}}\) ) A1 N1
[4 marks]
\({f^{(n)}}(x) = \frac{{{{( – 1)}^n}n!}}{{{x^{n + 1}}}}\) or \({( – 1)^n}n!({x^{ – (n + 1)}})\) A1A1A1 N3
[3 marks]
Question
Let \(f(x)=\ln x\)
(a) Find the first four derivatives of \(f(x)=\ln x\) and thus guess a formula for \(f^{(n)}(x)\).
(b) Prove by mathematical induction that your guess is true.
Answer/Explanation
Ans
The formula is \(f^{n}(x)=(-1)^{n+1}\frac{(n-1)!}{x^{n}}\)
Question
Let \(f(x)=e^{3x}\)
(a) Find the first four derivatives of \(f (x)\), and thus guess a formula for \(f^{(n)}(x)\)
(b) Prove by mathematical induction that your guess is true.
Answer/Explanation
Ans
The formula is \(f^{n}(x)=(3)^{n}e^{3x}\)
Question
(a) Show that for three functions it holds \((fgh)’=f’gh+fg’h+fgh’\)
(b) Generalize the product rule for \(n\) functions \(f_{1},f_{2},f_{3},…,f_{n}\).
Prove this formula by using mathematical induction.
Answer/Explanation
Ans
The formula is \((f_{1}f_{2}f_{3}…f_{n})’= f_{1}’f_{2}f_{3}…f_{n}+f_{1}f_{2}’f_{3}…f_{n}+…+f_{1}f_{2}f_{3}…f_{n}’\)
Question
Prove by mathematical induction that \(\frac{\mathrm{d} }{\mathrm{d} x}(x^{n})=nx^{n-1}\) for all positive integer values of \(n\).
Answer/Explanation
Ans
Let \(p_{n}\) be the statement \(\frac{\mathrm{d} }{\mathrm{d} x}=nx^{n-1}\) for all positive integer values of \(n\).
If \(n=1\) then \(\frac{\mathrm{d} }{\mathrm{d} x}(x^{1})= \lim_{x\rightarrow 0}\left ( \frac{(x+k)-x}{k} \right )=1=1x^{0}\)
Assume the formula is true for \(n =k\), that is \(\frac{\mathrm{d} }{\mathrm{d} x}(x^{k})=kx^{k-1}\).
Then \(\frac{\mathrm{d} }{\mathrm{d} x}(x^{k+1})=\frac{\mathrm{d} }{\mathrm{d} x}(x\times x^{k})=kx^{k-1}\times x+x^{k}=x^{k}(k+1)\)
which is the formula when \(n=k+1\)
So if the formula is true for \(n= k\) then it is true for \(n= k+1\).
\(p_{1}\) is true, therefore \(p_{n}\) is true for all integer values of \(n\).
Question
Using mathematical induction, prove that \(\frac{\mathrm{d^{n}} }{\mathrm{d} x^{n}}(\cos x)=\cos (x+\frac{n\pi }{2})\), for all positive integer values of \(n\).
Answer/Explanation
Ans
Let \(p_{n}\) be the statement for all positive integer values of \(n\).
For \(n= 1 p_{1}\) is true since, \(\frac{\mathrm{d} }{\mathrm{d} x}(cos x)=-\sin x= \cos \left ( x+ \frac{\pi }{2} \right )\)
Assume the formula is true for \(n= k\), that is, \(\frac{\mathrm{d^{k}} }{\mathrm{d} x^{k}}(\cos x)= \cos \left ( x+\frac{k\pi }{2} \right )\)
Then \(\frac{\mathrm{d^{k+1}} }{\mathrm{d} x^{k+1}}(\cos x)=\frac{\mathrm{d} }{\mathrm{d} x}\left ( \frac{\mathrm{d^{k}} }{\mathrm{d} x}(\cos x) \right )=\frac{\mathrm{d} }{\mathrm{d} x}\left ( \cos \left ( x+\frac{k\pi }{2} \right ) \right )=-\sin \left ( x+\frac{kx}{2} \right )\)
=\(\cos \left ( x+ \frac{kx}{2}+\frac{\pi }{2} \right )=\cos \left ( x+ \frac{(k+1)\pi }{2} \right )\)
which is \(p_{n}\) when \(n = k+1\).
(So if \(p_{n}\) is true for \(n =k\) then it is true for \(n =k+1)\) and by the principle of mathematical induction \(p_{n}\) is true for all positive integer values of \(n\).)
Question
The function \(f\) is defined by \(f(x)=xe^{2x}\)
Use mathematical induction to prove that \(f^{(n)}(x)=(2^{n}x+n2^{n-1})e^{2x}\) for all \(\ n\epsilon \mathbb{Z}\), where \(f^{(n)}(x)\) represents the \(n^{th}\) derivative of \(f(x)\).
Answer/Explanation
Ans
Show true for \(n =1\)
\(f'(x)=e^{2x}+2xe^{2x}\)
=\(e^{2x}(1+2x)= (2x+2^{0})e^{2x}\)
Assume true for \(n =k\), i.e. \(f^{(k)}x= (2^{k}x+k\times 2^{k-1})e^{2x}, k\geq 1\)
Consider \(n=k+1\), i.e. an attempt to find \(\frac{\mathrm{d} }{\mathrm{d} x}(f^{k}(x))\).
\((f^{k+1}(x))=2^{k}e^{2x}+2e^{2x}(2^{k}x+k\times 2^{k-1})\)
=\((2^{k}+2(2^{k}x+k\times 2^{k-1}))e^{2x}\)
=\((2\times 2^{k}x+2^{k}+k\times 2\times 2^{k-1})e^{2x}\)
=\((2^{k+1}x+2^{k}+k\times 2^{k})e^{2x}\)
=\((2^{k+1}x+(k+1)2^{k})e^{2x}\)
\(P(n)\) is true for \(k\Rightarrow P(n)\) is true for \(k+1\), and since true
for \(n =1\), result proved by mathematical induction \(\forall n\epsilon \mathbb{Z}^{+}\)
Question
(a) The function \(g\) is defined by \(g(x)=\frac{e^{x}}{\sqrt{x}}, for 0<x\leq 3\).
(ⅰ) Sketch the graph of \(g\).
(ⅰⅰ) Find \(g'(x)\).
(ⅰⅰⅰ) Write down an expression representing the gradient of the normal to the curve at any point.
(b) Let P be the point (x, y) on the graph of \(g\), and Q the point (1,0).
(ⅰ) Find the gradient of (PQ) in terms of \(x\).
(ⅰⅰ) Given that the line (PQ) is a normal to the graph of \(g\) at the point P, find the minimum distance from the point Q to the graph of \(g\).
Answer/Explanation
Ans
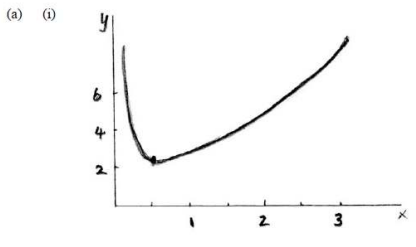
(ⅰⅰ) \(g(x)=\frac{e^{x}}{\sqrt{x}}\)
\(g'(x)= \frac{e^{x}\sqrt{x}-\frac{e^{x}}{2\sqrt{x}}}{x}\)
=\(\frac{(2x-1)e^{x}}{2x\sqrt{x}}\)
(ⅰⅰⅰ) gradient is \(\frac{1}{g'(x)}\)
\(=\frac{2x\sqrt{x}}{(1-2x)e^{x}}\)
(b) (ⅰ) \(\frac{y-0}{x-1}=\frac{e^{x}}{\sqrt{x}(x-1)}\)
(ⅰⅰ) EITHER
\(\frac{e^{x}}{\sqrt{x}(x-1)}=\frac{2x\sqrt{x}}{(1-2x)e^{x}}\)
\(x=0.5454 …\)
OR
\(D^{2}=(x-1)^{2}+y^{2}=(x-1)^{2}+\frac{e^{2x}}{x}\)
\(\frac{\mathrm{d} D^{2}}{\mathrm{d} x^{2}}=2(x-1)+\frac{2e^{2x}x-e^{2x}}{x^{2}}=0\)
\(x=0.5454 …\)
THEN
distance= \(\sqrt{(1-0.5454)^{2}+\left ( \frac{e^{0.5454}}{0.5454} \right )^{2}}\)
=\(2.38\)
Question
(a) Sketch and label the curves \(y=x^{2}\) for \(-2\leq x\leq 2\), and \(y= -\frac{1}{2}\ln x\) for \(0<x\leq 2\).
(b) Find the \(x\)-coordinate of P, the point of intersection of the two curves.
(c) If the tangents to the curves at P meet the \(y\)-axis at Q and R, calculate the area of the triangle PQR.
(d) Prove that the two tangents at the points where \(x=a, a>0\) on each curve are always perpendicular.
Answer/Explanation
Ans
(a) 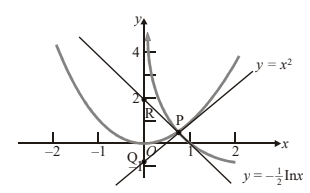
Question
Given that
(a) find \(\frac{\mathrm{d} y}{\mathrm{d} x}\)
(b) use mathematical induction to prove that, for \(n\epsilon \mathbb{Z^{+}}, \frac{\mathrm{d^{n}} y}{\mathrm{d} x^{n}}= (-1)^{n+1}e^{-x}(n-x)\)
Answer/Explanation
Ans
(a) \(y=xe^{-x}\)
\(\Rightarrow \frac{\mathrm{d} y}{\mathrm{d} x}=e^{-x}-xe^{-x} =e^{-x}(1-x)\)
(b) When \(n=1\), the formula gives \(\frac{\mathrm{d} y}{\mathrm{d} x}=(-1)^{2}e^{-x}(1-x)\)
=\(e^{-x}(1-x)\)
as demonstrated in part (a)
Assume true for \(n=k\)
\(\frac{\mathrm{d^{k}} y}{\mathrm{d} x^{k}}=(-1)^{k+1}e^{-x}(k-x)\)
Consider, \(\frac{\mathrm{d^{k+1}} y}{\mathrm{d} x^{k+1}}=\frac{\mathrm{d} }{\mathrm{d} x}\left [ (-1)^{k+1}e^{-x}(k-x) \right ]\)
=\((-1)^{k+1}\left [-e^{-x}(k-x)-e^{-x} \right ]\)
=\((-1)^{k+2}\left [e^{-x}(k+1-x) \right ]\)
Hence if it is true for \(k\), then it is true for \(k+1\)
Since the result is true for \(n=1\) and \(P(k)\Rightarrow P(k+1)\) the result is proved by
mathematical induction \(\forall \ n\epsilon \ \mathbb{Z}^{+}\)
Question
The function \(f\) is defined by \(f(x)= e^{nx}(x+1), here p\epsilon R\).
(i) Show that \(f'(x)= e^{nx}(p(x+1)+1)\).
(ii) Let \(f^{n}(x)\) denote the result of differentiating \(f (x)\) with respect to \(x\), \(n\) times.
Use mathematical induction to prove that
\(f^{n}(x)= p^{n-1}e^{nx}(p(x+1)+n), n\epsilon Z^{+}\).
Answer/Explanation
Ans
(i) \(f'(x)=pe^{px}(x+1)+e^{px}=e^{px}(p(x+1)+1)\)
(ii) The result is true for n=1 since
LHS = \(e^{px}(p(x+1)+1)\)\)
and RHS = \(p^{1-1}e^{px}(p(x+1)+1)=e^{px}(p(x+1)+1)\).
Assume true for \(n=k: f^{(k)}(x)=p^{k-1}e^{px}(p(x+1)+k)\)
\(f^{k+1}(x)=(f^{k}(x))’=p^{k-1}pe^{px}(p(x+1)+k)+p^{k-1}e^{px}p\)
=\(p^{k}e^{px}(p(x+1)+k+1)\)
Therefore, true for \(n=k\Rightarrow\) true for \(n=k+1\) and the proposition is proved by induction.
