Question:
The population, P, of a particular species of marsupial on a small remote island can be modelled by the logistic differential equation
\(\frac{dP}{dt}= kP\left ( 1-\frac{P}{N} \right )\)
where t is the time measured in years and k , N are positive constants.
The constant N represents the maximum population of this species of marsupial that the island can sustain indefinitely.
(a) In the context of the population model, interpret the meaning of \(\frac{dP}{dt}\).
(b) Show that \(\frac{d^{2}P}{dt^{2}}= k^{2}P\left ( 1-\frac{P}{N} \right )\left ( 1-\frac{2P}{N} \right )\)
(c) Hence show that the population of marsupials will increase at its maximum rate when \(P = \frac{N}{2}\). Justify your answer.
(d) Hence determine the maximum value of \(\frac{dP}{dt}\) in terms of k and N.
Let P0 be the initial population of marsupials.
(e) By solving the logistic differential equation, show that its solution can be expressed in the form
\(kt = In\frac{P}{P_{0}}\left ( \frac{N-P_{0}}{N-P} \right )\).
After 10 years, the population of marsupials is 3P0 . It is known that N = 4P0 .
(f) Find the value of k for this population model.
▶️Answer/Explanation
Ans:
(a) rate of growth (change) of the (marsupial) population (with respect to time)
Note: Do not accept growth (change) in the (marsupials) population per year.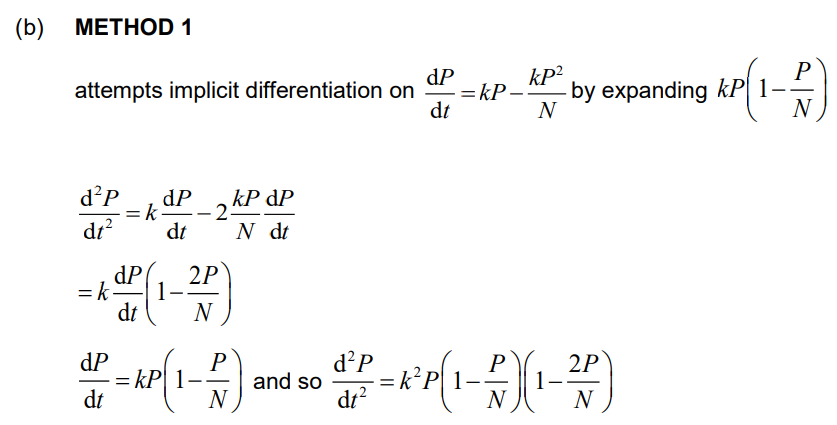


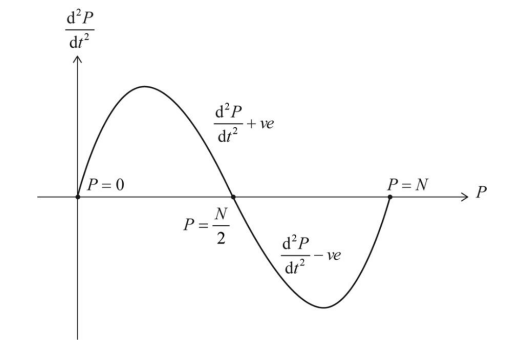
OR
a correct and clearly labelled sign diagram (table) showing \(P = \frac{N}{2}\) corresponding to a local maximum point for \(\frac{dP}{dt}\)
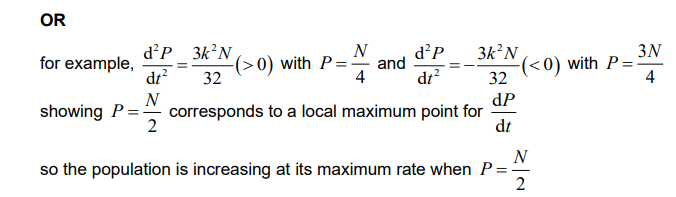
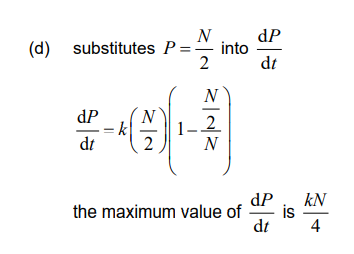


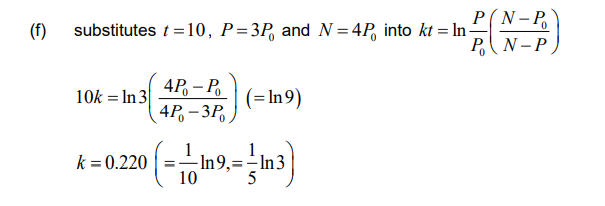
Question:
A scientist conducted a nine-week experiment on two plants, A and B, of the same species. He wanted to determine the effect of using a new plant fertilizer. Plant A was given fertilizer regularly, while Plant B was not.
The scientist found that the height of Plant A, hA cm, at time t weeks can be modelled by the function hA (t) = sin(2t + 6) + 9t + 27, where 0 ≤ t ≤ 9.
The scientist found that the height of Plant B, hB cm, at time t weeks can be modelled by the function hB (t) = 8t + 32, where 0 ≤ t ≤ 9.
(a) Use the scientist’s models to find the initial height of
(i) Plant B;
(ii) Plant A correct to three significant figures.
(b) Find the values of t when hA (t) = hB (t).
(c) For t > 6, prove that Plant A was always taller than Plant B.
(d) For 0 ≤ t ≤ 9, find the total amount of time when the rate of growth of Plant B was greater than the rate of growth of Plant A.
▶️Answer/Explanation
Ans:
(a) (i) 32 (cm)
(ii) hA (0) = sin (6) + 27
= 26.7205…
= 26.7 (cm)
(b) attempts to solve hA (t) = hB (t) for t
t = 4.0074…,4.7034…,5.88332…
t = 4.01,4.70,5.88 (weeks)
(c) hA (t) – hB (t) = sin (2t +6) +t -5
EITHER
for t > 6, t − 5 > 1
and as sin (2t +6) ≥-1 ⇒ hA (t) – hB (t) > 0
OR
the minimum value of sin (2t+6) = -1
so for t> 6, hA (t) – hB (t) = t -6 > 0
THEN
hence for t > 6, Plant A was always taller than Plant B
(d) recognises that hA‘ (t) and hB‘ (t) are required
attempts to solve hA‘ (t) = hB‘ (t) for t
t =1.18879… and 2.23598… OR 4.33038… and 5.37758… OR 7.47197… and 8.51917…

Question
The diagram below shows a circle with centre at the origin O and radius \(r > 0\) .
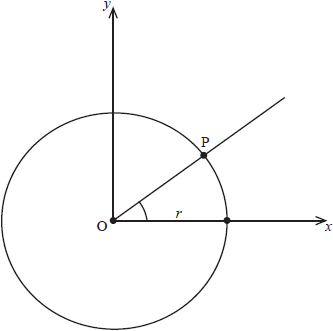
A point P(\(x\) , \(y\)) , (\(x > 0\), \(y > 0\)) is moving round the circumference of the circle.
Let \(m = \tan \left( {\arcsin \frac{y}{r}} \right)\) .
(a) Given that \(\frac{{{\text{d}}y}}{{{\text{d}}t}} = 0.001r\) , show that \(\frac{{{\text{d}}m}}{{{\text{d}}t}} = {\left( {\frac{r}{{10\sqrt {{r^2} – {y^2}} }}} \right)^3}\).
(b) State the geometrical meaning of \(\frac{{{\text{d}}m}}{{{\text{d}}t}}\) .
▶️/Explanation
Markscheme
(a) \(\frac{{{\text{d}}m}}{{{\text{d}}t}} = \frac{{{\text{d}}m}}{{{\text{d}}y}}\frac{{{\text{d}}y}}{{{\text{d}}t}}\) (M1)
\({ = {{\sec }^2}\left( {\arcsin \frac{y}{r}} \right) \times \left( {\arcsin \frac{y}{r}} \right)’ \times \frac{r}{{1000}}}\)
\( = \frac{1}{{{{\cos }^2}\left( {\arcsin \frac{y}{r}} \right)}} \times \frac{{\frac{1}{r}}}{{\sqrt {1 – {{\left( {\frac{y}{r}} \right)}^2}} }} \times \frac{r}{{1000}}\) (or equivalent) A1A1A1
\( = \frac{{\frac{1}{{\sqrt {{r^2} – {y^2}} }}}}{{\frac{{{r^2} – {y^2}}}{{{r^2}}}}}\frac{r}{{1000}}\) (A1)
\( = \frac{{{r^3}}}{{{{10}^3}\sqrt {{{\left( {{r^2} – {y^2}} \right)}^3}} }}\) (or equivalent) A1
\( = {\left( {\frac{r}{{10\sqrt {{r^2} – {y^2}} }}} \right)^3}\) AG N0
(b) \(\frac{{{\text{d}}m}}{{{\text{d}}t}}\) represents the rate of change of the gradient of the line OP A1
[7 marks]
Examiners report
Few students were able to complete this question successfully, although many did obtain partial marks. Many students failed to recognise the difference between differentiating with respect to \(t\) or with respect to \(y\) . Very few were able to give a satisfactory geometrical meaning in part (b).
Question
A helicopter H is moving vertically upwards with a speed of 10 ms−1 . The helicopter is \(h\) m directly above the point Q which is situated on level ground. The helicopter is observed from the point P which is also at ground level and PQ \( = 40\) m. This information is represented in the diagram below.
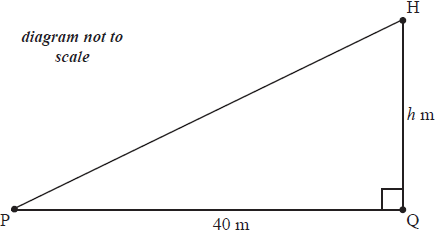
When \(h = 30\),
(a) show that the rate of change of \({\rm{H}}\hat {\text{P}}{\text{Q}}\) is \(0.16\) radians per second;
(b) find the rate of change of PH.
▶️Answer/Explanation
Markscheme
(a) let \({\text{H}}\hat {\text{P}}{\text{Q}} = \theta \)
\(\tan \theta = \frac{h}{{40}}\)
\({\sec ^2}\theta \frac{{{\text{d}}\theta }}{{{\text{d}}t}} = \frac{1}{{40}}\frac{{{\text{d}}h}}{{{\text{d}}t}}\) M1
\(\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = \frac{1}{{4{{\sec }^2}\theta }}\) (A1)
\( = \frac{{16}}{{4 \times 25}}\) \(\left( {\sec \theta = \frac{5}{4}{\text{ or }}\theta = 0.6435} \right)\) A1
\( = 0.16\) radians per second AG
(b) \({x^2} = {h^2} + 1600\), where PH \( = x\)
\(2x\frac{{{\text{d}}x}}{{{\text{d}}t}} = 2h\frac{{{\text{d}}h}}{{{\text{d}}t}}\) M1
\(\frac{{{\text{d}}x}}{{{\text{d}}t}} = \frac{h}{x} \times 10\) A1
\( = \frac{{10h}}{{\sqrt {{h^2} + 1600} }}\) (A1)
\(h = 30\) , \(\frac{{{\text{d}}x}}{{{\text{d}}t}} = 6\) ms–1 A1
Note: Accept solutions that begin\(x = 40\sec \theta \) or use \(h = 10t\) .
[7 marks]
Examiners report
For those candidates who realized this was an applied calculus problem involving related rates of change, the main source of error was in differentiating inverse tan in part (a). Some found part (b) easier than part (a), involving a changing length rather than an angle. A number of alternative approaches were reported by examiners.
Question
A stalactite has the shape of a circular cone. Its height is 200 mm and is increasing at a rate of 3 mm per century. Its base radius is 40 mm and is decreasing at a rate of 0.5 mm per century. Determine if its volume is increasing or decreasing, and the rate at which the volume is changing.
▶️Answer/Explanation
Markscheme
\(V = \frac{\pi }{3}{r^2}h\)
\(\frac{{{\text{d}}V}}{{{\text{d}}t}} = \frac{\pi }{3}\left[ {2rh\frac{{{\text{d}}r}}{{{\text{d}}t}} + {r^2}\frac{{{\text{d}}h}}{{{\text{d}}t}}} \right]\) M1A1A1
at the given instant
\(\frac{{{\text{d}}V}}{{{\text{d}}t}} = \frac{\pi }{3}\left[ {2(4)(200)\left( { – \frac{1}{2}} \right) + {{40}^2}(3)} \right]\) M1
\( = \frac{{ – 3200\pi }}{3} = – 3351.03 \ldots \approx 3350\) A1
hence, the volume is decreasing (at approximately 3350 \({\text{m}}{{\text{m}}^3}\) per century) R1
[6 marks]
Examiners report
Few candidates applied the method of implicit differentiation and related rates correctly. Some candidates incorrectly interpreted this question as one of constant linear rates.
Question
A ladder of length 10 m on horizontal ground rests against a vertical wall. The bottom of the ladder is moved away from the wall at a constant speed of \(0.5{\text{ m}}{{\text{s}}^{ – 1}}\). Calculate the speed of descent of the top of the ladder when the bottom of the ladder is 4 m away from the wall.
▶️Answer/Explanation
Markscheme
let x, y (m) denote respectively the distance of the bottom of the ladder from the wall and the distance of the top of the ladder from the ground
then,
\({x^2} + {y^2} = 100\) M1A1
\(2x\frac{{{\text{d}}x}}{{{\text{d}}t}} + 2y\frac{{{\text{d}}y}}{{{\text{d}}t}} = 0\) M1A1
when \(x = 4,{\text{ }}y = \sqrt {84} \) and \(\frac{{{\text{d}}x}}{{{\text{d}}t}} = 0.5\) A1
substituting, \(2 \times 4 \times 0.5 + 2\sqrt {84} \frac{{{\text{d}}y}}{{{\text{d}}t}} = 0\) A1
\(\frac{{{\text{d}}y}}{{{\text{d}}t}} = – 0.218{\text{ m}}{{\text{s}}^{ – 1}}\) A1
(speed of descent is \(0.218{\text{ m}}{{\text{s}}^{ – 1}}\))
[7 marks]
