Question 13. [Maximum mark: 8]
The graph below shows a small maze, in the form of a network of directed routes. The vertices A to F show junctions in the maze and the edges show the possible paths available from one vertex to another.
A mouse is placed at vertex A and left to wander the maze freely. The routes shown by dashed lines indicate paths sprinkled with sugar.
When the mouse reaches any junction, she rests for a constant time before continuing. At any junction, it may also be assumed that
the mouse chooses any available normal path with equal probability
if the junction includes a path sprinkled with sugar, the probability of choosing this path is twice that of a normal path.
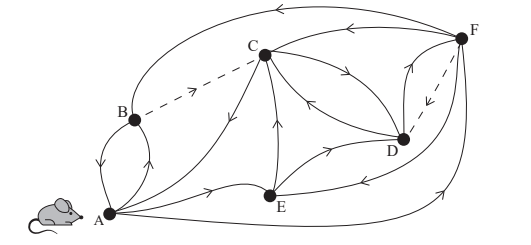
a. Determine the transition matrix for this graph. [3]
b. If the mouse was left to wander indefinitely, use your graphic display calculator to
estimate the percentage of time that the mouse would spend at point F. [3]
c. Comment on your answer to part (b), referring to at least one limitation of the model. [2]
▶️Answer/Explanation
(a) transition matrix is 
(b) attempting to raise the transition matrix to a large power steady state vector is 
so percentage of time spent at vertex F is 17.3%
(c) the model assumes instantaneous travel from junction to junction, and hence the answer obtained would be an overestimate OR the mouse may eat the sugar over time and hence the probabilities would change
Question 16. [Maximum mark: 5]
An ant is walking along the edges of a wire frame in the shape of a triangular prism.
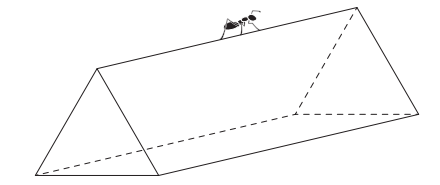
The vertices and edges of this frame can be represented by the graph below.
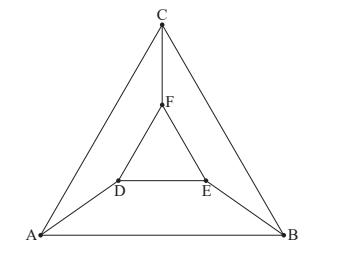
(a) Write down the adjacency matrix, M, for this graph. [3]
(b) Find the number of ways that the ant can start at the vertex A, and walk along exactly
6 edges to return to A. [2]
▶️Answer/Explanation
(a)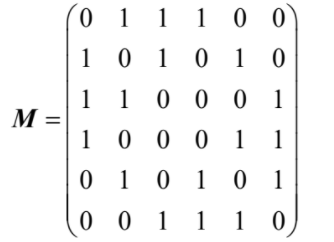 
Note: Award A1 for each two correct rows.
(b) calculating M6 =143
Question
A modern art painting is contained in a square frame. The painting has a shaded region
bounded by a smooth curve and a horizontal line.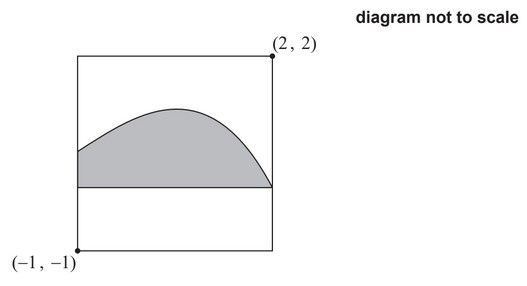
When the painting is placed on a coordinate axes such that the bottom left corner of the
painting has coordinates (−1, −1) and the top right corner has coordinates (2 , 2), the
curve can be modelled by y = f (x) and the horizontal line can be modelled by the x-axis.
Distances are measured in metres.
(a) Use the trapezoidal rule, with the values given in the following table, to approximate
the area of the shaded region.
| x | -1 | 0 | 1 | 2 |
| y | 0.6 | 1.2 | 1.2 | 0 |
The artist used the equation \(y=\frac{-x^3-3x^2+4x+12}{10}\) to draw the curve.
(b) Find the exact area of the shaded region in the painting.
(c) Find the area of the unshaded region in the painting.
▶️Answer/Explanation
Ans:
(a) \(\frac{1}{2}(0.6+0+2(1.2 + 1.2))\)
2.7 \(m^2\)
(b) \(\int_{-1}^{2}\frac{-x^3-3x^2+4x+12}{10}\) OR \(\int_{-1}^{2}f(x)dx\)
2.925 \(m^2\)
(c) 9-2.925
= 6.08 \(m^2\) (6.075)
Question
The graph G has adjacency matrix M given below.
a.Draw the graph G .[2]
b.What information about G is contained in the diagonal elements of M\(^2\) ?[1]
d.List the trails of length 4 starting at A and ending at C.[3]
▶️Answer/Explanation
Markscheme
A2
Note: Award A1 if only one error, A0 for two or more.
[2 marks]
the (k, k) element of M\(^2\) is the number of vertices directly connected to vertex k A1
Note: Accept comment about the number of walks of length 2, in which the initial and final vertices coincide.
[1 mark]
the trails of length 4 are ABEDC, AFEDC, AFEBC A1A1A1
Note: A1A1A1 for three correct with no additions; A1A1A0 for all correct, but with additions; A1A0A0 for two correct with or without additions.
[3 marks]