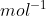Question
The table shows the variation of standard Gibbs energy with temperature for a reversible reaction.
∆G Θ= ∆H Θ – T∆S Θ
∆G Θ = – RT lnK
Temperature / K | ∆G Θ / kJ |
298 | 5.4 |
350 | –3.9 |
400 | –12.9 |
What can be concluded about the reaction?
A Equilibrium shifts left as temperature increases.
B The forward reaction is more spontaneous below 300 K.
C Entropy is higher in the products than in the reactants.
D Kc decreases as temperature increases.
▶️Answer/Explanation
C
If ΔG<0, the process occurs spontaneously. i.e. At temperatures above 298 K, the forward reaction is more spontaneous and the equilibrium shifts right as temperature increases. As temperature increases, ΔG becomes more negative and forward reaction is favoured more, hence Kc increases.
At 298 K, ΔG is positive but as temperature increases,ΔG becomes negative and more negative. It implies ΔS is positive for this reaction and entropy is higher in the products than in the reactants.
Question
Which reaction has the greatest increase in entropy?
A. \({{\text{C}}_3}{{\text{H}}_8}{\text{(g)}} + {\text{5}}{{\text{O}}_2}{\text{(g)}} \to {\text{3C}}{{\text{O}}_2}{\text{(g)}} + {\text{4}}{{\text{H}}_2}{\text{O(g)}}\)
B. \({{\text{H}}_2}{\text{(g)}} + {\text{C}}{{\text{l}}_2}{\text{(g)}} \to {\text{2HCl(g)}}\)
C. \({{\text{N}}_2}{\text{(g)}} + {\text{3}}{{\text{H}}_2}{\text{(g)}} \to {\text{2N}}{{\text{H}}_3}{\text{(g)}}\)
D. \({{\text{C}}_2}{{\text{H}}_4}{\text{(g)}} + {{\text{H}}_2}{\text{(g)}} \to {{\text{C}}_2}{{\text{H}}_6}{\text{(g)}}\)
▶️Answer/Explanation
A
Entropy increases when less moles of gases in reactants produce more number of moles of gases in products. In A, 6 moles of gases in reactants give 7 moles of gases in products. Hence, it has greatest increase in entropy.
Question
The reaction between but-1-ene and water vapour produces butan-1-ol.
\[{{\text{C}}_4}{{\text{H}}_8}{\text{(g)}} + {{\text{H}}_2}{\text{O(g)}} \to {{\text{C}}_4}{{\text{H}}_9}{\text{OH(l)}}\]
The standard entropy values \({\text{(}}{S^\Theta }{\text{)}}\) for but-1-ene, water vapour and butan-1-ol are 310, 189 and \({\text{228 J}}\,{{\text{K}}^{ – 1}}{\text{mo}}{{\text{l}}^{ – 1}}\) respectively. What is the standard entropy change for this reaction in \({\text{J}}\,{{\text{K}}^{ – 1}}{\text{mo}}{{\text{l}}^{ – 1}}\)?
A. –271
B. +271
C. –107
D. +107
▶️Answer/Explanation
A
ΔS∘rxn=S∘(C4H9OH)−[S∘(C4H8)+S∘(H20)]
ΔS∘rxn= 228-(310+189) = -271 \({\text{J}}\,{{\text{K}}^{ – 1}}{\text{mo}}{{\text{l}}^{ – 1}}\).
Question
A reaction has a standard enthalpy change, \(\Delta {H^\Theta }\), of \({\text{ +10.00 kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\) at 298 K. The standard entropy change, \(\Delta {S^\Theta }\), for the same reaction is \({\text{ +10.00 J}}\,{{\text{K}}^{ – 1}}{\text{mo}}{{\text{l}}^{ – 1}}\). What is the value of \(\Delta {G^\Theta }\) for the reaction in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\)?
A. +9.75
B. +7.02
C. –240
D. –2970
▶️Answer/Explanation
B
∆G = ∆H – T∆S = +10-298(+.010) = +7.02 \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\)
Question
What is the standard entropy change, \(\Delta {S^\Theta }\), for the following reaction?
\[{\text{2CO(g)}} + {{\text{O}}_2}{\text{(g)}} \to {\text{2C}}{{\text{O}}_2}{\text{(g)}}\]

A. –189
B. –173
C. +173
D. +189
▶️Answer/Explanation
B
ΔS∘rxn=2S∘(CO2)−[2S∘(CO)+S∘(O2)]
ΔS∘rxn= 2(214)-[2(198)+205] = -173 J/K/mol.
Question
Which change leads to an increase in entropy?
A. \({\text{C}}{{\text{O}}_{\text{2}}}{\text{(g)}} \to {\text{C}}{{\text{O}}_{\text{2}}}{\text{(s)}}\)
B. \({\text{S}}{{\text{F}}_6}({\text{g)}} \to {\text{S}}{{\text{F}}_6}({\text{l)}}\)
C. \({{\text{H}}_2}{\text{O(l)}} \to {{\text{H}}_2}{\text{O(s)}}\)
D. \({\text{NaCl(s)}} \to {\text{NaCl(aq)}}\)
▶️Answer/Explanation
D
As entropy of Solid<Liquid<Gas, entropy in D increases.