Download IITian Academy App for accessing Online Mock Tests and More..
Question
The weighted graph H is shown below.
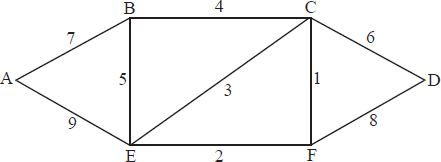
Use Kruskal’s Algorithm, indicating the order in which the edges are added, to find and draw the minimum spanning tree for H.
(i) A tree has v vertices. State the number of edges in the tree, justifying your answer.
(ii) We will call a graph with v vertices a “forest” if it consists of c components each of which is a tree.
Here is an example of a forest with 4 components.
How many edges will a forest with v vertices and c components have?
Answer/Explanation
Markscheme
The edges are included in the order
CF A1
EF A1
BC A1
CD A1
AB A1
A1
[6 marks]
(i) A tree with v vertices has v −1 edges. A1
Using v + f = e + 2 with f = 1, the result follows. R1
(ii) Each of the c trees will have one less edge than the number of vertices. R1
Thus the forest will have v − c edges. A2
[5 marks]
Examiners report
In (a), many candidates derived the minimum spanning tree although in some cases the method was not clearly indicated as required and some candidates used an incorrect algorithm. Part (b) was reasonably answered by many candidates although some justifications were unsatisfactory. Part (c) caused problems for many candidates who found difficulty in writing down a rigorous proof of the required result.
In (a), many candidates derived the minimum spanning tree although in some cases the method was not clearly indicated as required and some candidates used an incorrect algorithm. Part (b) was reasonably answered by many candidates although some justifications were unsatisfactory. Part (c) caused problems for many candidates who found difficulty in writing down a rigorous proof of the required result.
Question
Use Kruskal’s algorithm to find the minimum spanning tree for the following weighted graph and state its length.
Use Dijkstra’s algorithm to find the shortest path from A to D in the following weighted graph and state its length.
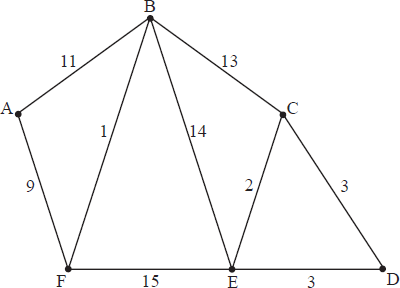
Answer/Explanation
Markscheme
Kruskal’s algorithm gives the following edges
CD (4) M1A1
AD (5)
EF (7) A1
EA (8)
BC (11)
FG (12) A1 N0
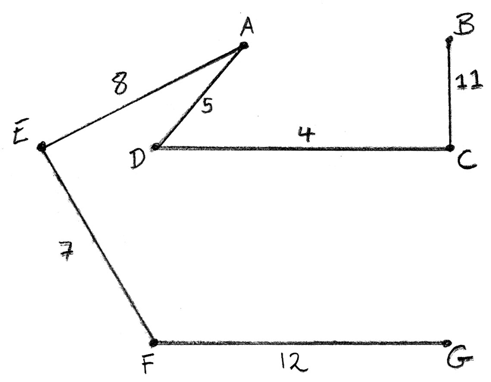
length of the spanning tree is 47 A1
[5 marks]
for Dijkstra’s algorithm there are three things associated with a node: order; distance from the initial node as a permanent or temporary node M1
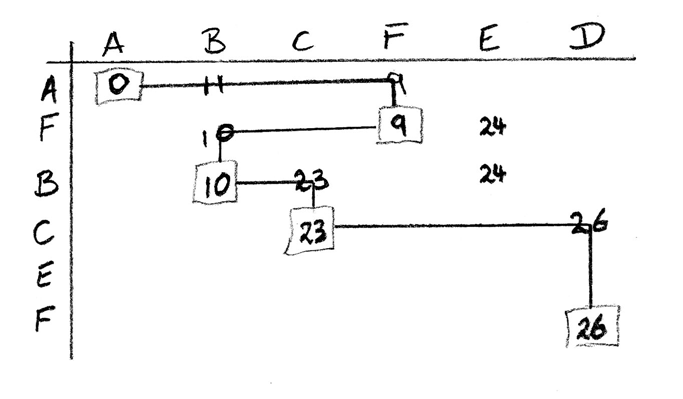A4
Note: Deduct A1 for each error or omission.
the shortest path is AFBCD A1
the length is 26 A1 N0
[7 marks]
Examiners report
Setting out clearly the steps of the algorithms is still a problem for many although getting the correct spanning tree and its length were not.
Setting out clearly the steps of the algorithms is still a problem for many although getting the correct spanning tree and its length were not.
Question
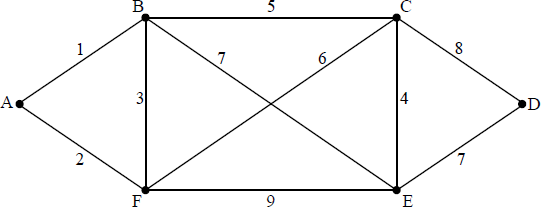
Sameer is trying to design a road system to connect six towns, A, B, C, D, E and F. The possible roads and the costs of building them are shown in the graph below. Each vertex represents a town, each edge represents a road and the weight of each edge is the cost of building that road. He needs to design the lowest cost road system that will connect the six towns.
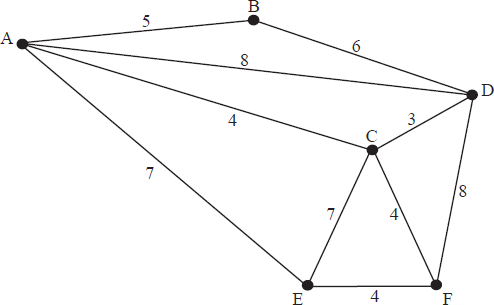
(a) Name an algorithm which will allow Sameer to find the lowest cost road system.
(b) Find the lowest cost road system and state the cost of building it. Show clearly the steps of the algorithm.
Answer/Explanation
Answer/Explanation
Markscheme
(a) EITHER
Prim’s algorithm A1
OR
Kruskal’s algorithm A1
[1 mark]
(b) EITHER
using Prim’s algorithm, starting at A
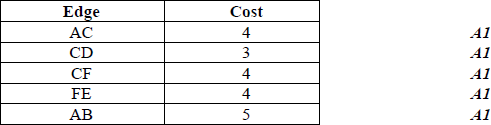
lowest cost road system contains roads AC, CD, CF, FE and AB A1
cost is 20 A1
OR
using Kruskal’s algorithm
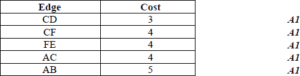
lowest cost road system contains roads CD, CF, FE, AC and AB A1
cost is 20 A1
Note: Accept alternative correct solutions.
[7 marks]
Total [8 marks]
Examiners report
Most candidates were able to name an algorithm to find the lowest cost road system and then were able apply the algorithm. All but the weakest candidates were able to make a meaningful start to this question. In 1(b) some candidates lost marks by failing to indicate the order in which edges were added.
Question
The diagram below shows the weighted graph G .
(a) (i) What feature of the graph enables you to deduce that G contains an Eulerian circuit?
(ii) Find an Eulerian circuit.
(c) Use Kruskal’s Algorithm to find the minimum spanning tree for G , showing the order in which the edges are added.
Answer/Explanation
Markscheme
(a) (i) all the vertices have even degree A1
(ii) for example ABCDECFBEFA A2
[3 marks]
(c) the edges are included in the order shown
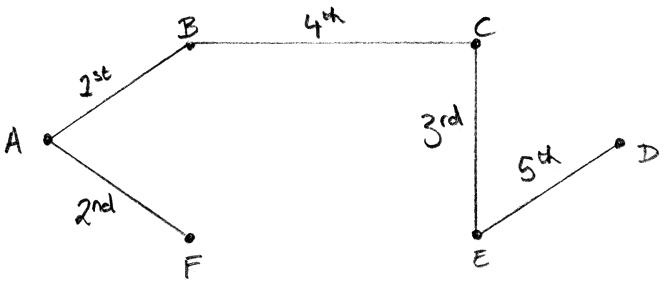M1A1A1A1A1A1
Note: Award each A1 for the edge added in the correct order. Award no further marks after the first error.
[6 marks]
Total [9 marks]
Examiners report
Part (a) was well answered in general. Part (c) was well answered.
Question
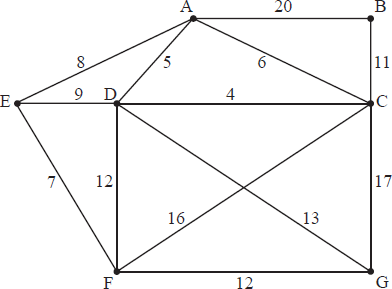
A graph G with vertices A, B, C, D, E has the following cost adjacency table.
\[\begin{array}{*{20}{c|ccccc}}
{}&{\text{A}}&{\text{B}}&{\text{C}}&{\text{D}}&{\text{E}} \\
\hline
{\text{A}}& – &{12}&{10}&{17}&{19} \\
{\text{B}}&{12}& – &{13}&{20}&{11} \\
{\text{C}}&{10}&{13}& – &{16}&{14} \\
{\text{D}}&{17}&{20}&{16}& – &{15} \\
{\text{E}}&{19}&{11}&{14}&{15}& –
\end{array}\]
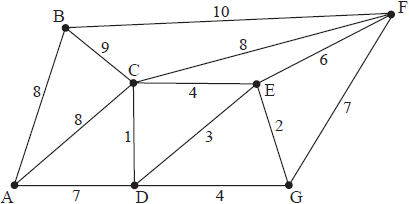
(a) (i) Use Kruskal’s algorithm to find and draw the minimum spanning tree for G.
(ii) The graph H is formed from G by removing the vertex D and all the edges connected to D. Draw the minimum spanning tree for H and use it to find a lower bound for the travelling salesman problem for G.
(b) Show that 80 is an upper bound for this travelling salesman problem.
Answer/Explanation
Markscheme
(a) (i) the edges are joined in the order
AC
BE
AB
ED A2
A1
Note: Final A1 independent of the previous A2.
(ii)
A1
the weight of this spanning tree is 33 A1
to find a lower bound for the travelling salesman problem, we add to that the two smallest weights of edges to D, i.e. 15 +16, giving 64 M1A1
[7 marks]
(b) an upper bound is the weight of any Hamiltonian cycle, e.g. ABCDEA has weight 75 so 80 is certainly an upper bound M1A1
[2 marks]
Total [9 marks]
Examiners report
Part (a) was well done by many candidates although some candidates simply drew the minimum spanning tree in (i) without indicating the use of Kruskal’s Algorithm. It is important to stress to candidates that, as indicated in the rubric at the top of Page 2, answers must be supported by working and/or explanations. Part (b) caused problems for some candidates who obtained the unhelpful upper bound of 96 by doubling the weight of the minimum spanning tree. It is useful to note that the weight of any Hamiltonian cycle is an upper bound and in this case it was fairly easy to find such a cycle with weight less than or equal to 80.
Question
Consider the following weighted graph.
(a) (i) Use Kruskal’s algorithm to find the minimum spanning tree. Indicate the order in which you select the edges and draw the final spanning tree.
(ii) Write down the total weight of this minimum spanning tree.
(b) Sketch a spanning tree of maximum total weight and write down its weight.
Answer/Explanation
Markscheme
(a) (i) (Kruskal’s: successively take an edge of smallest weight without forming a cycle)
\({1^{{\text{st}}}}\) edge DC (weight 1) A1
\({2^{{\text{nd}}}}\) edge EG (weight 2) A1
\({3^{{\text{rd}}}}\) edge DE (weight 3) A1
\({4^{{\text{th}}}}\) edge EF (weight 6) A1
\({5^{{\text{th}}}}\) edge AD (weight 7) A1
\({6^{{\text{th}}}}\) edge AB (weight 8) A1
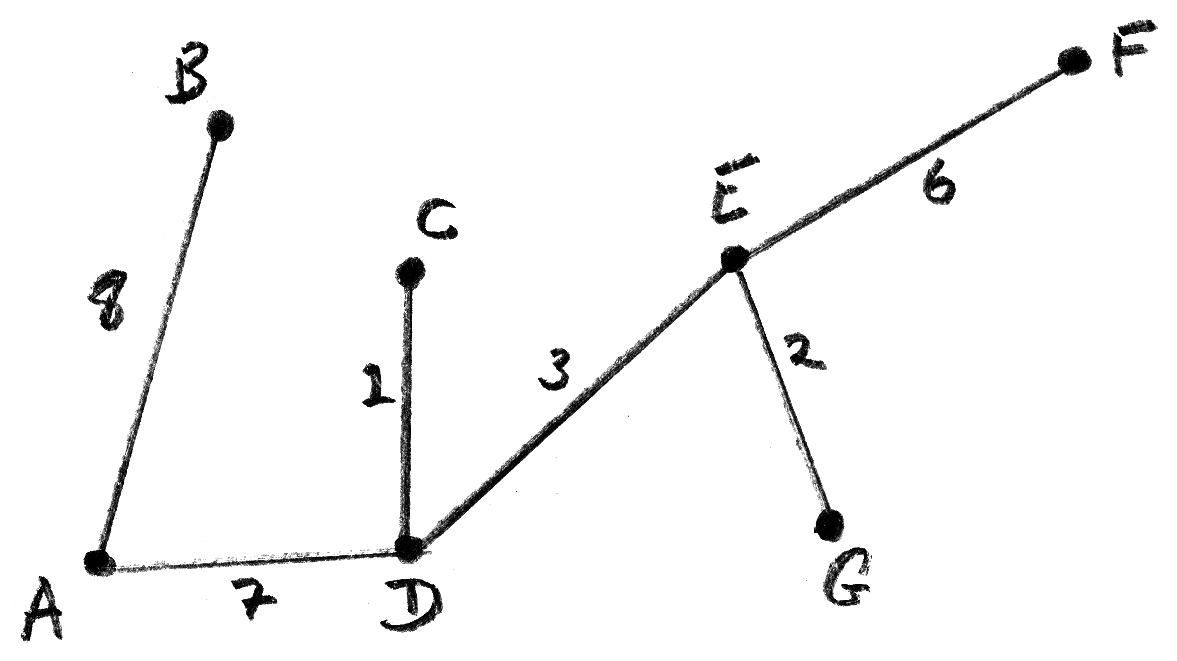A1
Notes: Weights are not required on the diagram.
Allow A2(d) if the (correct) edges are in the wrong order e.g. they have used Prim’s rather than Kruskal’s algorithm.
(ii) total weight is 1 + 2 + 3 + 6 + 7 + 8 = 27 A1
[8 marks]
(b) EITHER
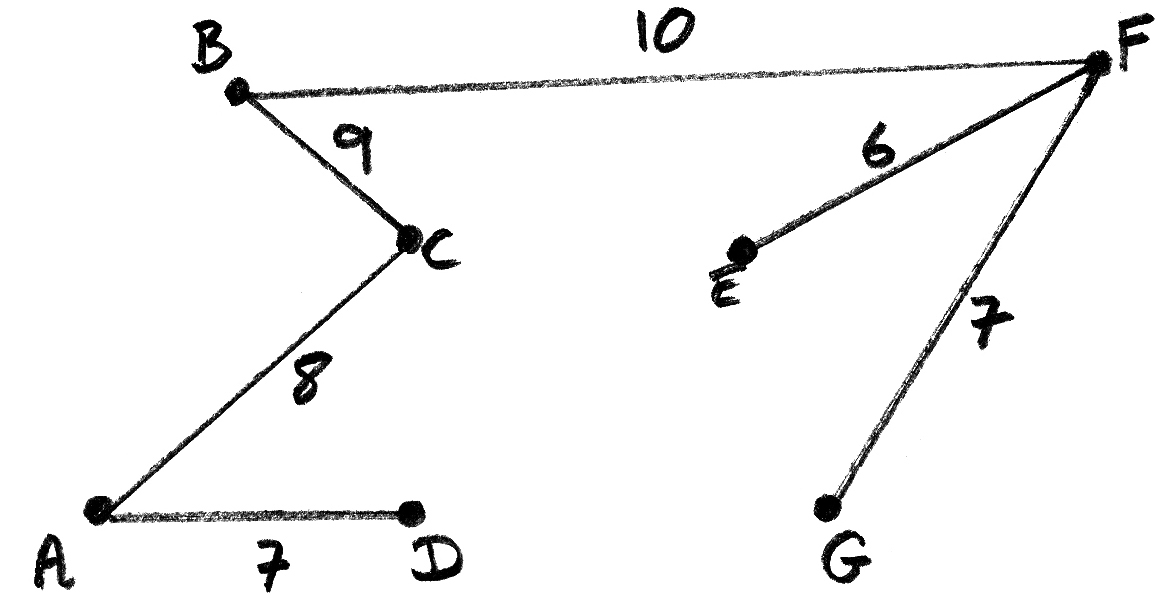A3
OR
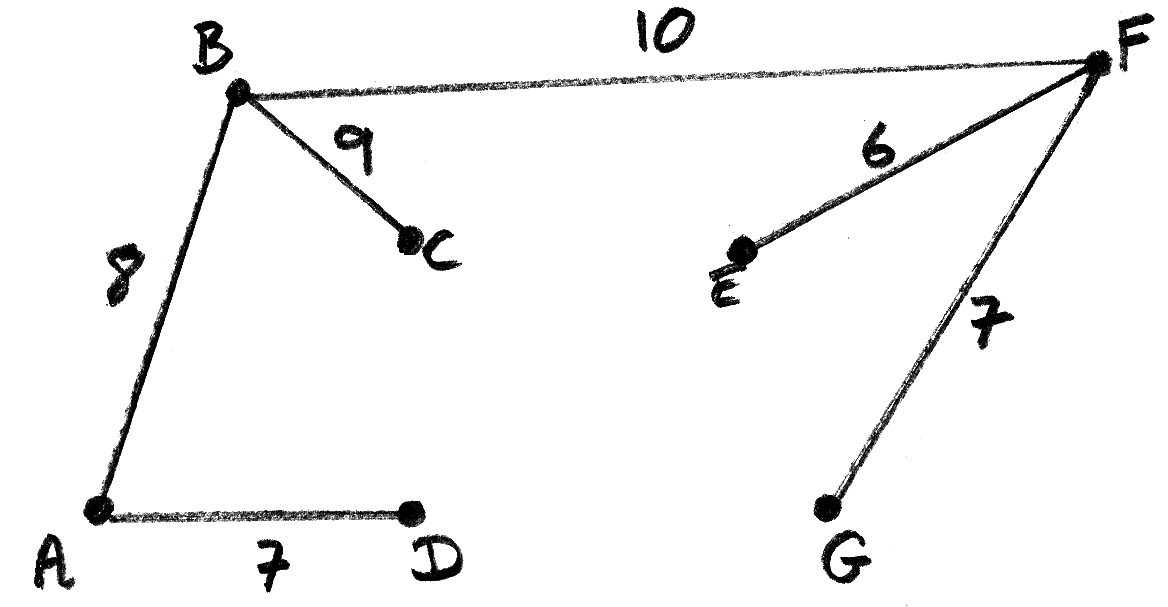A3
Notes: Award A2 for five or four correct edges,
A1 for three or two correct edges
A0 otherwise.
Weights are not required on the diagram.
THEN
total weight is 6 + 7 + 7 + 8 + 9 + 10 = 47 A1
[4 marks]
Total [12 marks]
Examiners report
Good algorithm work was shown; sometimes there were mistakes in giving the order of the edges chosen by, for example doing Prim’s algorithm instead of Kruskal’s.
Question
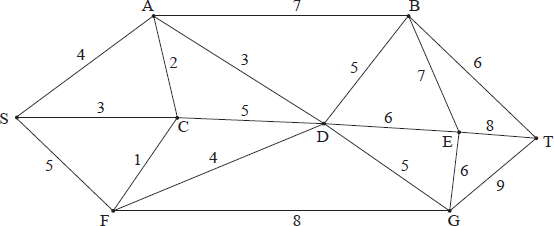
In the graph given above, the numbers shown represent the distance along that edge.
Using Dijkstra’s algorithm, find the length of the shortest path from vertex S to vertex T . Write down this shortest path.
(i) Does this graph have an Eulerian circuit? Justify your answer.
(ii) Does this graph have an Eulerian trail? Justify your answer.
The graph above is now to be considered with the edges representing roads in a town and with the distances being the length of that road in kilometres. Huan is a postman and he has to travel along every road in the town to deliver letters to all the houses in that road. He has to start at the sorting office at S and also finish his route at S . Find the shortest total distance of such a route. Fully explain the reasoning behind your answer.
Answer/Explanation
Markscheme
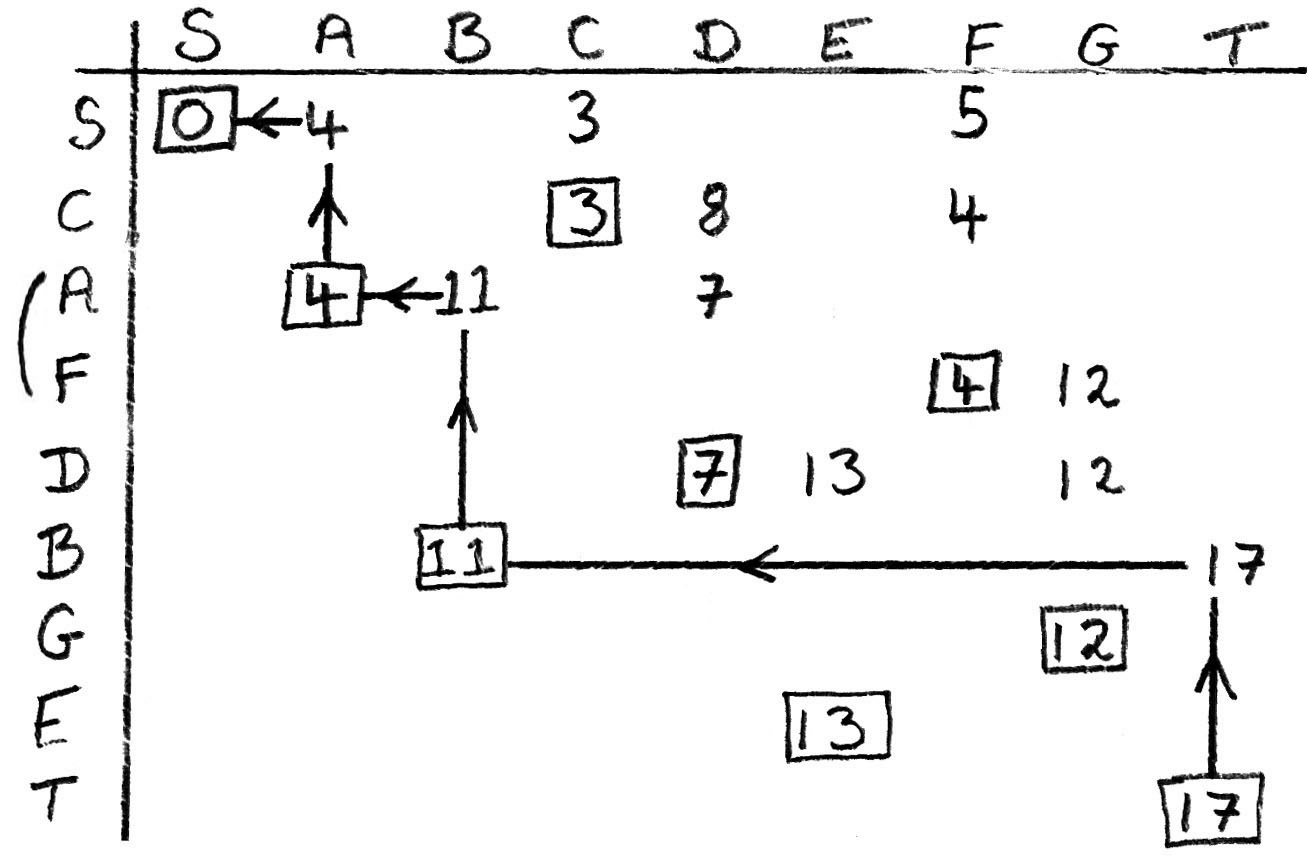
from tabular method as shown above (or equivalent) M1A1A1
Note: Award the first A1 for obtaining 3 as the shortest distance to C.
Award the second A1 for obtaining the rest of the shortest distances.
shortest path has length 17 A1
backtracking as shown above (or equivalent) (M1)
shortest path is SABT A1
[6 marks]
(i) no, as S and T have odd degree A1R1
Note: Mentioning one vertex of odd degree is sufficient.
(ii) yes, as only S and T have odd degree A1R1
Note: In each case only award the A1 if the R1 has been given.
Accept an actual trail in (b)(ii).
[4 marks]
Huan has to travel along all the edges via an open Eulerian trail of length R1
4 + 3 + 5 + 2 + 1 + 3 + 5 + 4 + 7 + 8 + 5 + 6 + 7 + 6 + 6 + 8 + 9 = 94 A1
and then back to S from T along the shortest path found in (a) of length 17 R1
so shortest total distance is 94 + 17 = 111 A1
[4 marks]
Examiners report
This was quite well answered. Some candidates did not make their method clear and others showed no method at all. Some clearly had a correct method but did not make it clear what their final answers were. It is recommended that teachers look at the tabular method with its backtracking system as shown in the mark scheme as an efficient way of tackling this type of problem.
Fairly good knowledge shown here but not by all.
Some good answers but too much confusion with methods they partly remembered about the travelling salesman problem. Candidates should be aware of helpful connections between parts of a question.
Question
The diagram shows a weighted graph with vertices A, B, C, D, E, F, G. The weight of each edge is marked on the diagram.
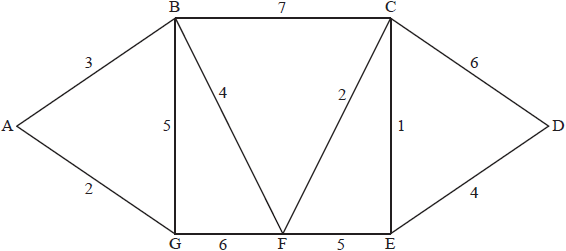
(i) Explain briefly why the graph contains an Eulerian trail but not an Eulerian circuit.
(ii) Write down an Eulerian trail.
(i) Use Dijkstra’s algorithm to find the path of minimum total weight joining A to D.
(ii) State the minimum total weight.
Answer/Explanation
Markscheme
(i) there is an Eulerian trail because there are only 2 vertices of odd degree R1
there is no Eulerian circuit because not all vertices have even degree R1
(ii) eg GBAGFBCFECDE A2
[4 marks]
(i)
\(\begin{array}{*{20}{l}}
{{\text{Step}}}&{{\text{Vertices labelled}}}&{{\text{Working values}}}&{} \\
1&{\text{A}}&{{\text{A(0), B-3, G-2}}}&{{\boldsymbol{M1A1}}} \\
2&{{\text{A, G}}}&{{\text{A(0), G(2), B-3, F-8}}}&{{\boldsymbol{A1}}} \\
3&{{\text{A, G, B}}}&{{\text{A(0), G(2), B(3), F-7, C-10}}}&{{\boldsymbol{A1}}} \\
4&{{\text{A, G, B, F}}}&{{\text{A(0), G(2), B(3), F(7), C-9, E-12}}}&{} \\
5&{{\text{A, G, B, F, C}}}&{{\text{A(0), G(2), B(3), F(7), C(9), E-10, D-15}}}&{{\boldsymbol{A1}}} \\
6&{{\text{A, G, B, F, C, E}}}&{{\text{A(0), G(2), B(3), F(7), C(9), E(10), D-14}}}&{} \\
7&{{\text{A, G, B, F, C, E, D}}}&{{\text{A(0), G(2), B(3), F(7), C(9), E(10), D(14)}}}&{{\boldsymbol{A1}}}
\end{array}\)
Note: In both (i) and (ii) accept the tabular method including back tracking or labels by the vertices on a graph.
Note: Award M1A1A1A1A0A0 if final labels are correct but intermediate ones are not shown.
(ii) minimum weight path is ABFCED A1
minimum weight is 14 A1
Note: Award the final two A1 marks whether or not Dijkstra’s Algorithm is used.
[8 marks]
Examiners report
In part (a) the criteria for Eulerian circuits and trails were generally well known and most candidates realised that they must start/finish at G/E. Candidates who could not do (a) generally struggled on the paper.
For part (b) the layout varied greatly from candidate to candidate. Not all candidates made their method clear and some did not show the temporary labels. It is recommended that teachers look at the tabular method with its backtracking system as it is an efficient way of tackling this type of problem and has a very clear layout.
Question
The following diagram shows a weighted graph.
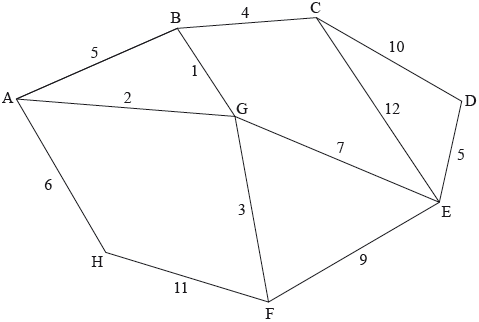
(a) Use Kruskal’s algorithm to find a minimum spanning tree, clearly showing the order in which the edges are added.
(b) Sketch the minimum spanning tree found, and write down its weight.
Answer/Explanation
Markscheme
(a) use Kruskal’s algorithm: begin by choosing the shortest edge and then select a sequence of edges of non-decreasing weights, checking at each stage that no cycle is completed (M1)
| choice | edge | weight |
| 1 | BG | 1 |
| 2 | AG | 2 |
| 3 | FG | 3 |
| 4 | BC | 4 |
| 5 | DE | 5 |
| 6 | AH | 6 |
| 7 | EG | 7 |
A1
A3
Note: A1 for steps 2–4, A1for step 5 and A1for steps 6, 7.
Award marks only if it is clear that Kruskal’s algorithm is being used.
[5 marks]
(b) weight \( = 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28\) A1
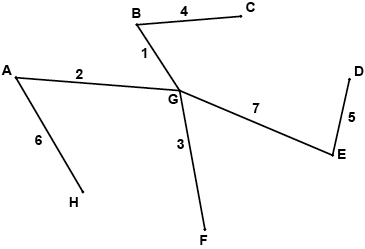A1
Note: Award FT only if it is a spanning tree.
[2 marks]
Examiners report
Well answered by the majority of candidates.
Question
The following graph represents the cost in dollars of travelling by bus between 10 towns in a particular province.
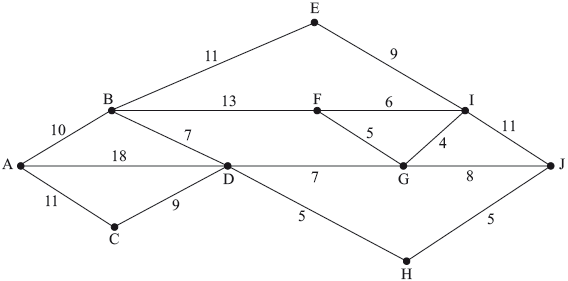
Use Dijkstra’s algorithm to find the cheapest route between \(A\) and \(J\), and state its cost.
For the remainder of the question you may find the cheapest route between any two towns by inspection.
It is given that the total cost of travelling on all the roads without repeating any is \(\$ 139\).
A tourist decides to go over all the roads at least once, starting and finishing at town \(A\).
Find the lowest possible cost of his journey, stating clearly which roads need to be travelled more than once. You must fully justify your answer.
Answer/Explanation
Markscheme
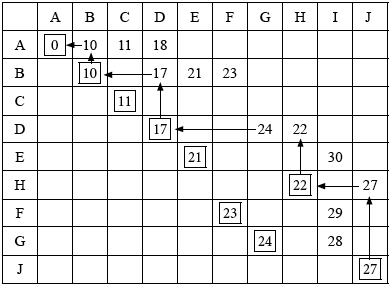M1A1A1A1
(M1 for an attempt at Dijkstra’s)
(A1 for value of \({\text{D}} = 17\))
(A1 for value of \({\text{H}} = 22\))
(A1 for value of \({\text{G}} = 22\))
route is \(ABDHJ\) (M1)A1
cost is \($27\) A1
Note: Accept other layouts.
[7 marks]
there are 4 odd vertices \(A\), \(D\), \(F\) and \(J\) A1
these can be joined up in 3 ways with the following extra costs
\(AD\) and \(FJ\)\(\;\;\;17 + 13 = 30\)
\(AF\) and \(DJ\)\(\;\;\;23 + 10 = 33\)
\(AJ\) and \(DF\)\(\;\;\;27 + 12 = 39\) M1A1A1
Note: Award M1 for an attempt to find different routes.
Award A1A1 for correct values for all three costs A1 for one correct.
need to repeat \(AB\), \(BD\), \(FG\) and \(GJ\) A1
total cost is \(139 + 30 = \$ 169\) A1
[6 marks]
Total [13 marks]
Examiners report
Many candidates had the correct route and the cost. Not all showed sufficient working with their Dijkstra’s algorithm. See the mark-scheme for the neat way of laying out the working, including the back-tracking method. This tabular working is efficient, avoids mistakes and saves time.
There was often confusion here between this problem and the travelling salesman. Good candidates started with the number of vertices of odd degree. Weaker candidates just tried to write the answer down without complete reasoning. All the 3 ways of joining the odd vertices had to be considered so that you knew you had the smallest. Sometimes a mark was lost by giving which routes (paths) had to be repeated rather than which roads (edges).
Question
The weights of the edges of a graph \(H\) are given in the following table.
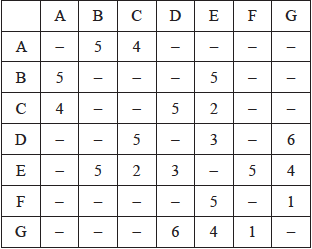
(i) Draw the weighted graph \(H\).
(ii) Use Kruskal’s algorithm to find the minimum spanning tree of \(H\). Your solution should indicate the order in which the edges are added.
(iii) State the weight of the minimum spanning tree.
Consider the following weighted graph.
(i) Write down a solution to the Chinese postman problem for this graph.
(ii) Calculate the total weight of the solution.
(i) State the travelling salesman problem.
(ii) Explain why there is no solution to the travelling salesman problem for this graph.
Answer/Explanation
Markscheme
(i)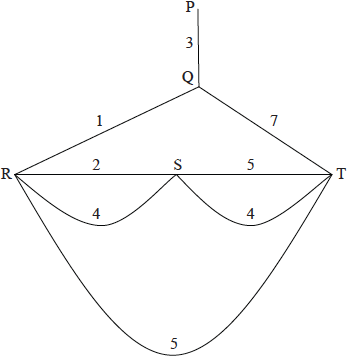 
A2
Note: Award A1 if one edge is missing. Award A1 if the edge weights are not labelled.
(ii) the edges are added in the order:
\(FG{\rm{ }}1\) M1A1
\(CE{\rm{ }}2\) A1
\(ED{\rm{ }}3\)
\(EG{\rm{ }}4\) A1
\(AC{\rm{ }}4\)
Note: \(EG\) and \(AC\) can be added in either order.
(Reject \(EF\))
(Reject \(CD\))
\(EB5\) OR \(AB5\) A1
Notes: The minimum spanning tree does not have to be seen.
If only a tree is seen, the order by which edges are added must be clearly indicated.
(iii) \(19\) A1
[8 marks]
(i) eg, \(PQRSRTSTQP\) OR \(PQTSTRSRQP\) M1A1
Note: Award M1 if in either (i) or (ii), it is recognised that edge \(PQ\) is needed twice.
(ii) total weight \( = 34\) A1
[3 marks]
(i) to determine a cycle where each vertex is visited once only (Hamiltonian cycle) A1
of least total weight A1
(ii) EITHER
to reach \(P\), \(Q\) must be visited twice which contradicts the definition of the \(TSP\) R1
OR
the graph is not a complete graph and hence there is no solution to the \(TSP\) R1
[3 marks]
Total [14 marks]
Examiners report
Part (a) was generally very well answered. Most candidates were able to correctly sketch the graph of \(H\) and apply Kruskal’s algorithm to determine the minimum spanning tree of \(H\). A few candidates used Prim’s algorithm (which is no longer part of the syllabus).
Most candidates understood the Chinese Postman Problem in part (b) and knew to add the weight of \(PQ\) to the total weight of \(H\). Some candidates, however, did not specify a solution to the Chinese Postman Problem while other candidates missed the fact that a return to the initial vertex is required.
In part (c), many candidates had trouble succinctly stating the Travelling Salesman Problem. Many candidates used an ‘edge’ argument rather than simply stating that the Travelling Salesman Problem could not be solved because to reach vertex \(P\), vertex \(Q\) had to be visited twice.
Question
The distances by road, in kilometres, between towns in Switzerland are shown in the following table.
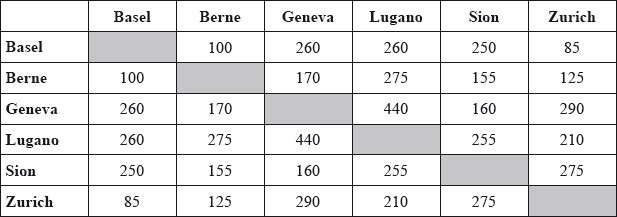
A cable television company wishes to connect the six towns placing cables along the road system.
Use Kruskal’s algorithm to find the minimum length of cable needed to connect the six towns.
Visitors to Switzerland can visit some principal locations for tourism by using a network of scenic railways as represented by the following graph:
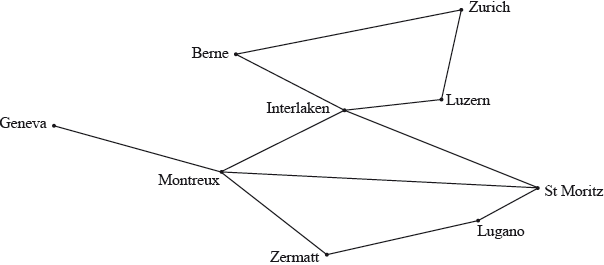
(i) State whether the graph has any Hamiltonian paths or Hamiltonian cycles, justifying your answers.
(ii) State whether the graph has any Eulerian trails or Eulerian circuits, justifying your answers.
(iii) The tourist board would like to make it possible to arrive in Geneva, travel all the available scenic railways, exactly once, and depart from Zurich. Find which locations would need to be connected by a further scenic railway in order to make this possible.
Answer/Explanation
Markscheme
Zurich-Basel 85 M1A1
Berne-Basel 100 A1
Sion-Berne 155
Sion-Geneva 160
Zurich-Lugano 210 A1
total length of pipe needed is 710 km A1
Note: Award M1 for attempt to start with smallest length.
Note: Accept graphical solution showing lengths chosen.
Note: Award N1 for a correct spanning tree and N1 for 710 km with no method shown.
[6 marks]
(i) possible Hamiltonian path eg Geneva-Montreux-Zermatt-Lugano-St Moritz-Interlaken-Luzern-Zurich-Berne A1
no possible Hamiltonian cycles eg we would have to pass through Montreux twice as Geneva is only connected to Montreux or Interlaken twice R1
(ii) possible Eulerian trail as there are 2 odd vertices (Geneva and St Moritz) R1
no possible Eulerian circuits as not all even vertices R1
Note: Accept an example of a Eulerian trail for the first R1.
(iii) St Moritz to Zurich A2
Note: If St Moritz and Zurich are connected via existing edges award A1.
[6 marks]
Total [11 marks]
Examiners report
[N/A]
[N/A]
Question
The weights of the edges in the complete graph \(G\) are shown in the following table.
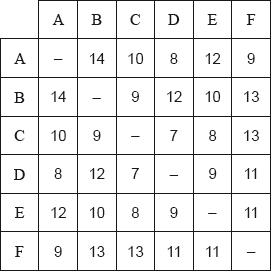
Starting at A, use the nearest neighbour algorithm to find an upper bound for the travelling salesman problem for \(G\).
By first removing A , use the deleted vertex algorithm to find a lower bound for the travelling salesman problem for \(G\).
Answer/Explanation
Markscheme
attempt to use the nearest neighbour algorithm M1
\(\begin{array}{*{20}{l}} {{\text{the nearest neighbour path is}}}&{{\text{A}} \to {\text{D}} \to {\text{C }}A1} \\ {}&{ \to {\text{E}} \to {\text{B}} \to {\text{F}} \to {\text{A }}A1} \end{array}\)
the upper bound is the total weight of this path, ie (M1)
\(8 + 7 + 8 + 10 + 13 + 9 = 55\) A1
Note: The (M1) is for adding 6 weights together.
[5 marks]
attempt to use an appropriate algorithm, with A deleted, to determine the minimum spanning tree, eg Kruskal’s (M1)
CD (7) A1
CE, CB (8,9) A1
DF or EF (11) A1
the weight of this minimum spanning tree is 35 (A1)
adding in the two smallest weights joining A (AD and AF) to this tree gives a lower bound (M1)
of \(35 + 8 + 9 = 52\) A1
Note: Clear diagrams aiding solutions are acceptable in (a) and (b).
[7 marks]
Examiners report
Generally good use of the nearest neighbour algorithm. Some candidates showed no knowledge of it and there was some confusion with the twice the weight of a minimal spanning tree method. Some candidates forgot to go back to A and thus did not have a Hamiltonian cycle.
The method was generally known. Some candidates used nearest neighbour instead of Kruskal’s algorithm to find a minimal spanning tree. Some forgot to add in the two edges connected to . Some with the right method made mistakes in not noticing the correct edge to choose. A
Question
The simple, complete graph \({\kappa _n}(n > 2)\) has vertices \({{\text{A}}_1},{\text{ }}{{\text{A}}_2},{\text{ }}{{\text{A}}_3},{\text{ }} \ldots ,{\text{ }}{{\text{A}}_n}\). The weight of the edge from \({{\text{A}}_i}\) to \({{\text{A}}_j}\) is given by the number \(i + j\).
Consider the general graph \({\kappa _n}\).
(i) Draw the graph \({\kappa _4}\) including the weights of all the edges.
(ii) Use the nearest-neighbour algorithm, starting at vertex \({{\text{A}}_1}\), to find a Hamiltonian cycle.
(iii) Hence, find an upper bound to the travelling salesman problem for this weighted graph.
Consider the graph \({\kappa _5}\). Use the deleted vertex algorithm, with \({{\text{A}}_5}\) as the deleted vertex, to find a lower bound to the travelling salesman problem for this weighted graph.
(i) Use the nearest-neighbour algorithm, starting at vertex \({{\text{A}}_1}\), to find a Hamiltonian cycle.
(ii) Hence find and simplify an expression in \(n\), for an upper bound to the travelling salesman problem for this weighted graph.
By splitting the weight of the edge \({{\text{A}}_i}{{\text{A}}_j}\) into two parts or otherwise, show that all Hamiltonian cycles of \({\kappa _n}\) have the same total weight, equal to the answer found in (c)(ii).
Answer/Explanation
Markscheme
(i)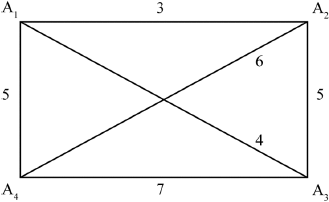 
A1A1
Note: A1 for the graph, A1 for the weights.
(ii) cycle is \({{\text{A}}_1}{{\text{A}}_2}{{\text{A}}_3}{{\text{A}}_4}{{\text{A}}_1}\) A1
(iii) upper bound is \(3 + 5 + 7 + 5 = 20\) A1
[4 marks]
with \({{\text{A}}_5}\) deleted, (applying Kruskal’s Algorithm) the minimum spanning tree will consist of the edges \({{\text{A}}_1}{{\text{A}}_2},{\text{ }}{{\text{A}}_1}{{\text{A}}_3}{\text{, }}{{\text{A}}_1}{{\text{A}}_4}\), of weights 3, 4, 5 (M1)A1
the two edges of smallest weight from \({{\text{A}}_5}\) are \({{\text{A}}_5}{{\text{A}}_1}\) and \({{\text{A}}_5}{{\text{A}}_2}\) of weights 6 and 7 (M1)A1
so lower bound is \(3 + 4 + 5 + 6 + 7 = 25\) A1
[5 marks]
(i) starting at \({{\text{A}}_1}\) we go \({{\text{A}}_2},{\text{ }}{{\text{A}}_3}{\text{ }} \ldots {\text{ }}{{\text{A}}_n}\)
we now have to take \({{\text{A}}_n}{{\text{A}}_1}\)
thus the cycle is \({{\text{A}}_1}{{\text{A}}_2}{{\text{A}}_3} \ldots {{\text{A}}_{n – 1}}{{\text{A}}_n}{{\text{A}}_1}\) A1A1
Note: Final A1 is for \({{\text{A}}_n}{{\text{A}}_1}\).
(ii) smallest edge from \({{\text{A}}_1}\) is \({{\text{A}}_1}{{\text{A}}_2}\) of weight 3, smallest edge from \({{\text{A}}_2}\) (to a new vertex) is \({{\text{A}}_2}{{\text{A}}_3}\) of weight 5, smallest edge from \({{\text{A}}_{n – 1}}\) (to a new vertex) is \({{\text{A}}_{n – 1}}{{\text{A}}_n}\) of weight \(2n – 1\) (M1)
weight of \({{\text{A}}_n}{{\text{A}}_1}\) is \(n + 1\)
weight is \(3 + 5 + 7 + \ldots + (2n – 1) + (n + 1)\) A1
\( = \frac{{(n – 1)}}{2}(2n + 2) + (n + 1)\) M1A1
\( = n(n + 1)\) (which is an upper bound) A1
Note: Follow through is not applicable.
[7 marks]
put a marker on each edge \({{\text{A}}_i}{{\text{A}}_j}\) so that \(i\) of the weight belongs to vertex \({{\text{A}}_i}\) and \(j\) of the weight belongs to vertex \({{\text{A}}_j}\) M1
the Hamiltonian cycle visits each vertex once and only once and for vertex \({{\text{A}}_i}\) there will be weight \(i\) (belonging to vertex \({{\text{A}}_i}\)) both going in and coming out R1
so the total weight will be \(\sum\limits_{i = 1}^n {2i = 2\frac{n}{2}(n + 1) = n(n + 1)} \) A1AG
Note: Accept other methods for example induction.
[3 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
Question
The weights of the edges of a graph G with vertices A, B, C, D and E are given in the following table.
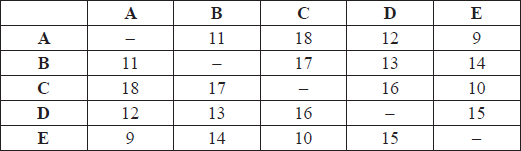
Starting at A, use the nearest neighbour algorithm to find an upper bound for the travelling salesman problem for G .
(i) Use Kruskal’s algorithm to find and draw a minimum spanning tree for the subgraph obtained by removing the vertex A from G .
(ii) Hence use the deleted vertex algorithm to find a lower bound for the travelling salesman problem for G .
Answer/Explanation
Markscheme
using the nearest neighbour algorithm, starting with A,
\({\text{A}} \to {\text{E, E}} \to {\text{C}}\) A1
\({\text{C}} \to {\text{D, D}} \to {\text{B}}\) A1
\({\text{B}} \to {\text{A}}\) A1
the upper bound is therefore 9 + 10 + 16 + 13 + 11 = 59 A1
[4 marks]
(i) the edges are added in the order CE A1
BD A1
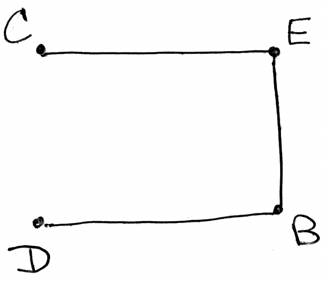BE A1
A1
(ii) the weight of the minimum spanning tree is 37 (A1)
we now reconnect A with the 2 edges of least weight (M1)
i.e. AE and AB A1
the lower bound is therefore 37 + 9 + 11 = 57 A1
[8 marks]
Examiners report
[N/A]
[N/A]