Question
The function \(f\) is defined by \(f\left( x \right) = \frac{{ax + b}}{{cx + d}}\), for \(x \in \mathbb{R},\,\,x \ne – \frac{d}{c}\).
The function \(g\) is defined by \(g\left( x \right) = \frac{{2x – 3}}{{x – 2}},\,\,x \in \mathbb{R},\,\,x \ne 2\)
Find the inverse function \({f^{ – 1}}\), stating its domain.[5]
Express \(g\left( x \right)\) in the form \(A + \frac{B}{{x – 2}}\) where A, B are constants.[2]
Sketch the graph of \(y = g\left( x \right)\). State the equations of any asymptotes and the coordinates of any intercepts with the axes.[3]
The function \(h\) is defined by \(h\left( x \right) = \sqrt x \), for \(x\) ≥ 0.
State the domain and range of \(h \circ g\).[4]
Answer/Explanation
Markscheme
attempt to make \(x\) the subject of \(y = \frac{{ax + b}}{{cx + d}}\) M1
\(y\left( {cx + d} \right) = ax + b\) A1
\(x = \frac{{dy – b}}{{a – cy}}\) A1
\({f^{ – 1}}\left( x \right) = \frac{{dx – b}}{{a – cx}}\) A1
Note: Do not allow \(y = \) in place of \({f^{ – 1}}\left( x \right)\).
\(x \ne \frac{a}{c},\,\,\,\left( {x \in \mathbb{R}} \right)\) A1
Note: The final A mark is independent.
[5 marks]
\(g\left( x \right) = 2 + \frac{1}{{x – 2}}\) A1A1
[2 marks]
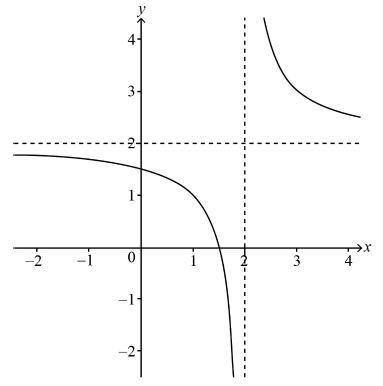
hyperbola shape, with single curves in second and fourth quadrants and third quadrant blank, including vertical asymptote \(x = 2\) A1
horizontal asymptote \(y = 2\) A1
intercepts \(\left( {\frac{3}{2},\,0} \right),\,\left( {0,\,\frac{3}{2}} \right)\) A1
[3 marks]
the domain of \(h \circ g\) is \(x \leqslant \frac{3}{2},\,\,x > 2\) A1A1
the range of \(h \circ g\) is \(y \geqslant 0,\,\,y \ne \sqrt 2 \) A1A1
[4 marks]
