Question
Two non-intersecting circles C1 , containing points M and S , and C2 , containing points N and R, have centres P and Q where PQ \( = 50\) . The line segments [MN] and [SR] are common tangents to the circles. The size of the reflex angle MPS is \( \alpha\), the size of the obtuse angle NQR is \( \beta\) , and the size of the angle MPQ is \( \theta\) . The arc length MS is \({l_1}\) and the arc length NR is \({l_2}\) . This information is represented in the diagram below.
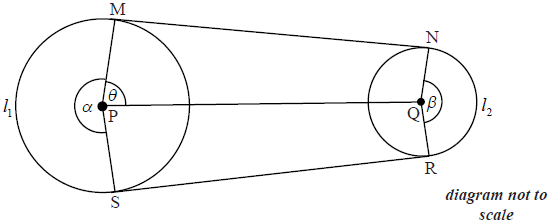
The radius of C1 is \(x\) , where \(x \geqslant 10\) and the radius of C2 is \(10\).
(a) Explain why \(x < 40\) .
(b) Show that cosθ = x −10 50.
(c) (i) Find an expression for MN in terms of \(x\) .
(ii) Find the value of \(x\) that maximises MN.
(d) Find an expression in terms of \(x\) for
(i) \( \alpha\) ;
(ii) \( \beta\) .
(e) The length of the perimeter is given by \({l_1} + {l_2} + {\text{MN}} + {\text{SR}}\).
(i) Find an expression, \(b (x)\) , for the length of the perimeter in terms of \(x\) .
(ii) Find the maximum value of the length of the perimeter.
(iii) Find the value of \(x\) that gives a perimeter of length \(200\).
Answer/Explanation
Markscheme
(a) PQ \( = 50\) and non-intersecting R1
[1 mark]
(b) a construction QT (where T is on the radius MP), parallel to MN, so that \({\text{Q}}\hat {\text{T}}{\text{M}} = 90^\circ \) (angle between tangent and radius \( = 90^\circ \) ) M1
lengths \(50\), \(x – 10\) and angle \( \theta\) marked on a diagram, or equivalent R1
Note: Other construction lines are possible.
[2 marks]
(c) (i) MN \( = \sqrt {{{50}^2} – {{\left( {x – 10} \right)}^2}} \) A1
(ii) maximum for MN occurs when \(x = 10\) A1
[2 marks]
(d) (i) \(\alpha = 2\pi – 2\theta \) M1
\( = 2\pi – 2\arccos \left( {\frac{{x – 10}}{{50}}} \right)\) A1
(ii) \(\beta = 2\pi – \alpha \) ( \( = 2\theta \) ) A1
\( = 2\left( {{{\cos }^{ – 1}}\left( {\frac{{x – 10}}{{50}}} \right)} \right)\) A1
[4 marks]
(e) (i) \(b(x) = x\alpha + 10\beta + 2\sqrt {{{50}^2} – {{\left( {x – 10} \right)}^2}} \) A1A1A1
\( = x\left( {2\pi – 2\left( {{{\cos }^{ – 1}}\left( {\frac{{x – 10}}{{50}}} \right)} \right)} \right) + 20\left( {\left( {{{\cos }^{ – 1}}\left( {\frac{{x – 10}}{{50}}} \right)} \right)} \right) + 2\sqrt {{{50}^2} – {{\left( {x – 10} \right)}^2}} \) M1A1
(ii) maximum value of perimeter \( = 276\) A2
(iii) perimeter of \(200\) cm \(b(x) = 200\) (M1)
when \(x = 21.2\) A1
[9 marks]
Total [18 marks]
Examiners report
This is not an inherently difficult question, but candidates either made heavy weather of it or avoided it almost entirely. The key to answering the question is in obtaining the displayed answer to part (b), for which a construction line parallel to MN through Q is required. Diagrams seen by examiners on some scripts tend to suggest that the perpendicularity property of a tangent to a circle and the associated radius is not as firmly known as they had expected. Some candidates mixed radians and degrees in their expressions.
Question
An electricity station is on the edge of a straight coastline. A lighthouse is located in the sea 200 m from the electricity station. The angle between the coastline and the line joining the lighthouse with the electricity station is 60°. A cable needs to be laid connecting the lighthouse to the electricity station. It is decided to lay the cable in a straight line to the coast and then along the coast to the electricity station. The length of cable laid along the coastline is x metres. This information is illustrated in the diagram below.
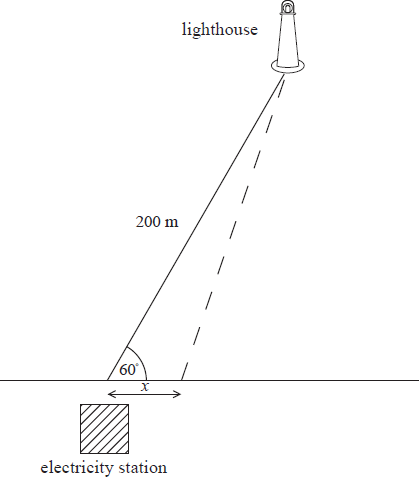
The cost of laying the cable along the sea bed is US$80 per metre, and the cost of laying it on land is US$20 per metre.
Find, in terms of x, an expression for the cost of laying the cable.
Find the value of x, to the nearest metre, such that this cost is minimized.
Answer/Explanation
Markscheme
let the distance the cable is laid along the seabed be y
\({y^2} = {x^2} + {200^2} – 2 \times x \times 200\cos 60^\circ \) (M1)
(or equivalent method)
\({y^2} = {x^2} – 200x + 40000\) (A1)
cost = C = 80y + 20x (M1)
\(C = 80{({x^2} – 200x + 40000)^{\frac{1}{2}}} + 20x\) A1
[4 marks]
\(x = 55.2786 \ldots = 55\) (m to the nearest metre) (A1)A1
\(\left( {x = 100 – \sqrt {2000} } \right)\)
[2 marks]
Examiners report
Some surprising misconceptions were evident here, using right angled trigonometry in non right angled triangles etc. Those that used the cosine rule, usually managed to obtain the correct answer to part (a).
Some surprising misconceptions were evident here, using right angled trigonometry in non right angled triangles etc. Many students attempted to find the value of the minimum algebraically instead of the simple calculator solution.
Question
Engineers need to lay pipes to connect two cities A and B that are separated by a river of width 450 metres as shown in the following diagram. They plan to lay the pipes under the river from A to X and then under the ground from X to B. The cost of laying the pipes under the river is five times the cost of laying the pipes under the ground.
Let \({\text{EX}} = x\).
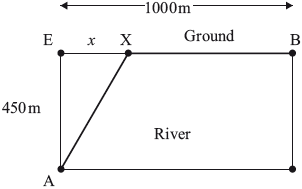
Let k be the cost, in dollars per metre, of laying the pipes under the ground.
(a) Show that the total cost C, in dollars, of laying the pipes from A to B is given by \(C = 5k\sqrt {202\,500 + {x^2}} + (1000 – x)k\).
(b) (i) Find \(\frac{{{\text{d}}C}}{{{\text{d}}x}}\).
(ii) Hence find the value of x for which the total cost is a minimum, justifying that this value is a minimum.
(c) Find the minimum total cost in terms of k.
The angle at which the pipes are joined is \({\rm{A\hat XB}} = \theta \).
(d) Find \(\theta \) for the value of x calculated in (b).
For safety reasons \(\theta \) must be at least 120°.
Given this new requirement,
(e) (i) find the new value of x which minimises the total cost;
(ii) find the percentage increase in the minimum total cost.
Answer/Explanation
Markscheme
(a) \(C = {\text{AX}} \times 5k + {\text{XB}} \times k\) (M1)
Note: Award (M1) for attempting to express the cost in terms of AX, XB and k.
\( = 5k\sqrt {{{450}^2} + {x^2}} + (1000 – x)k\) A1
\( = 5k\sqrt {202\,500 + {x^2}} + (1000 – x)k\) AG
[2 marks]
(b) (i) \(\frac{{{\text{d}}C}}{{{\text{d}}x}} = k\left[ {\frac{{5 \times 2x}}{{2\sqrt {202\,500 + {x^2}} }} – 1} \right] = k\left( {\frac{{5x}}{{\sqrt {202\,500 + {x^2}} }} – 1} \right)\) M1A1
Note: Award M1 for an attempt to differentiate and A1 for the correct derivative.
(ii) attempting to solve \(\frac{{{\text{d}}C}}{{{\text{d}}x}} = 0\) M1
\(\frac{5}{{\sqrt {202\,500 + {x^2}} }} = 1\) (A1)
\(x = 91.9{\text{ (m) }}\left( { = \frac{{75\sqrt 6 }}{2}{\text{ (m)}}} \right)\) A1
METHOD 1
for example,
at \(x = 91\frac{{{\text{d}}C}}{{{\text{d}}x}} = – 0.00895k < 0\) M1
at \(x = 92\frac{{{\text{d}}C}}{{{\text{d}}x}} = 0.001506k > 0\) A1
Note: Award M1 for attempting to find the gradient either side of \(x = 91.9\) and A1 for two correct values.
thus \(x = 91.9\) gives a minimum AG
METHOD 2
\(\frac{{{{\text{d}}^2}C}}{{{\text{d}}{x^2}}} = \frac{{1\,012\,500k}}{{{{\left( {{x^2} + 202\,500} \right)}^{\frac{3}{2}}}}}\)
at \(x = 91.9\frac{{{{\text{d}}^2}C}}{{{\text{d}}{x^2}}} = 0.010451k > 0\) (M1)A1
Note: Award M1 for attempting to find the second derivative and A1 for the correct value.
Note: If \(\frac{{{{\text{d}}^2}C}}{{{\text{d}}{x^2}}}\) is obtained and its value at \(x = 91.9\) is not calculated, award (M1)A1 for correct reasoning eg, both numerator and denominator are positive at \(x = 91.9\).
thus \(x = 91.9\) gives a minimum AG
METHOD 3
Sketching the graph of either C versus x or \(\frac{{{\text{d}}C}}{{{\text{d}}x}}\) versus x. M1
Clearly indicating that \(x = 91.9\) gives the minimum on their graph. A1
[7 marks]
(c) \({C_{\min }} = 3205k\) A1
Note: Accept 3200k.
Accept 3204k.
[1 mark]
(d) \(\arctan \left( {\frac{{450}}{{91.855865{\text{K}}}}} \right) = 78.463{\text{K}}^\circ \) M1
\(180 – 78.463{\text{K = 101.537K}}\)
\( = 102^\circ \) A1
[2 marks]
(e) (i) when \(\theta = 120^\circ ,{\text{ }}x = 260{\text{ (m) }}\left( {\frac{{450}}{{\sqrt 3 }}{\text{ (m)}}} \right)\) A1
(ii) \(\frac{{133.728{\text{K}}}}{{3204.5407685{\text{K}}}} \times 100\% \) M1
\( = 4.17{\text{ (% )}}\) A1
[3 marks]
Total [15 marks]
Examiners report
Question
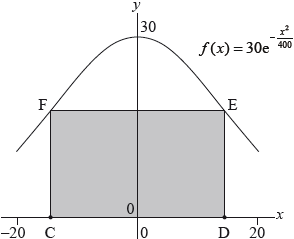
The following diagram shows a vertical cross section of a building. The cross section of the roof of the building can be modelled by the curve \(f(x) = 30{{\text{e}}^{ – \frac{{{x^2}}}{{400}}}}\), where \( – 20 \le x \le 20\).
Ground level is represented by the \(x\)-axis.
Find \(f”(x)\).
Show that the gradient of the roof function is greatest when \(x = – \sqrt {200} \).
The cross section of the living space under the roof can be modelled by a rectangle \(CDEF\) with points \({\text{C}}( – a,{\text{ }}0)\) and \({\text{D}}(a,{\text{ }}0)\), where \(0 < a \le 20\).
Show that the maximum area \(A\) of the rectangle \(CDEF\) is \(600\sqrt 2 {{\text{e}}^{ – \frac{1}{2}}}\).
A function \(I\) is known as the Insulation Factor of \(CDEF\). The function is defined as \(I(a) = \frac{{P(a)}}{{A(a)}}\) where \({\text{P}} = {\text{Perimeter}}\) and \({\text{A}} = {\text{Area of the rectangle}}\).
(i) Find an expression for \(P\) in terms of \(a\).
(ii) Find the value of \(a\) which minimizes \(I\).
(iii) Using the value of \(a\) found in part (ii) calculate the percentage of the cross sectional area under the whole roof that is not included in the cross section of the living space.
Answer/Explanation
Markscheme
\(f'(x) = 30{{\text{e}}^{ – \frac{{{x^2}}}{{400}}}} \bullet – \frac{{2x}}{{400}}\;\;\;\left( { = – \frac{{3x}}{{20}}{{\text{e}}^{ – \frac{{{x^2}}}{{400}}}}} \right)\) M1A1
Note: Award M1 for attempting to use the chain rule.
\(f”(x) = – \frac{3}{{20}}{{\text{e}}^{ – \frac{{{x^2}}}{{400}}}} + \frac{{3{x^2}}}{{4000}}{{\text{e}}^{ – \frac{{{x^2}}}{{400}}}}\;\;\;\left( { = \frac{3}{{20}}{{\text{e}}^{ – \frac{{{x^2}}}{{400}}}}\left( {\frac{{{x^2}}}{{200}} – 1} \right)} \right)\) M1A1
Note: Award M1 for attempting to use the product rule.
[4 marks]
the roof function has maximum gradient when \(f”(x) = 0\) (M1)
Note: Award (M1) for attempting to find \(f”\left( { – \sqrt {200} } \right)\).
EITHER
\( = 0\) A1
OR
\(f”(x) = 0 \Rightarrow x = \pm \sqrt {200} \) A1
THEN
valid argument for maximum such as reference to an appropriate graph or change in the sign of \(f”(x)\) eg \(f”( – 15) = 0.010 \ldots ( > 0)\) and \(f”( – 14) = – 0.001 \ldots ( < 0)\) R1
\( \Rightarrow x = – \sqrt {200} \) AG
[3 marks]
\(A = 2a \bullet 30{{\text{e}}^{ – \frac{{{a^2}}}{{400}}}}\;\;\;\left( { = 60a{{\text{e}}^{ – \frac{{{a^2}}}{{400}}}} = – 400g'(a)} \right)\) (M1)(A1)
EITHER
\(\frac{{{\text{d}}A}}{{{\text{d}}a}} = 60a{{\text{e}}^{ – \frac{{{a^2}}}{{400}}}} \bullet – \frac{a}{{200}} + 60{{\text{e}}^{ – \frac{{{a^2}}}{{400}}}} = 0 \Rightarrow a = \sqrt {200} {\text{ }}\left( { – 400f”(a) = 0 \Rightarrow a = \sqrt {200} } \right)\) M1A1
OR
by symmetry eg \(a = – \sqrt {200} \) found in (b) or \({A_{{\text{max}}}}\) coincides with \(f”(a) = 0\) R1
\( \Rightarrow a = \sqrt {200} \) A1
Note: Award A0(M1)(A1)M0M1 for candidates who start with \(a = \sqrt {200} \) and do not provide any justification for the maximum area. Condone use of \(x\).
THEN
\({A_{{\text{max}}}} = 60 \bullet \sqrt {200} {{\text{e}}^{ – \frac{{200}}{{400}}}}\) M1
\( = 600\sqrt 2 {{\text{e}}^{ – \frac{1}{2}}}\) AG
[5 marks]
(i) perimeter \( = 4a + 60{{\text{e}}^{ – \frac{{{a^2}}}{{400}}}}\) A1A1
Note: Condone use of \(x\).
(ii) \(I(a) = \frac{{4a + 60{{\text{e}}^{ – \frac{{{a^2}}}{{400}}}}}}{{60a{{\text{e}}^{ – \frac{{{a^2}}}{{400}}}}}}\) (A1)
graphing \(I(a)\) or other valid method to find the minimum (M1)
\(a = 12.6\) A1
(iii) area under roof \( = \int_{ – 20}^{20} {30{{\text{e}}^{ – \frac{{{x^2}}}{{400}}}}} {\text{d}}x\) M1
\( = 896.18 \ldots \) (A1)
area of living space \( = 60 \cdot (12.6…) \cdot e – {\frac{{(12.6…)}}{{400}}^2} = 508.56…\)
percentage of empty space \( = 43.3\% \) A1
[9 marks]
Total [21 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
Question
Points A , B and T lie on a line on an indoor soccer field. The goal, [AB] , is 2 metres wide. A player situated at point P kicks a ball at the goal. [PT] is perpendicular to (AB) and is 6 metres from a parallel line through the centre of [AB] . Let PT be \(x\) metros and let \(\alpha = {\rm{A\hat PB}}\) measured in degrees. Assume that the ball travels along the floor.
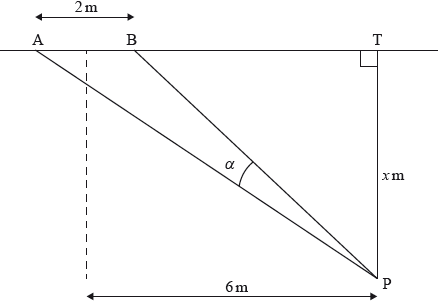
The maximum for \(\tan \alpha \) gives the maximum for \(\alpha \).
Find the value of \(\alpha \) when \(x = 10\).
Show that \(\tan \alpha = \frac{{2x}}{{{x^2} + 35}}\).
(i) Find \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha )\).
(ii) Hence or otherwise find the value of \(\alpha \) such that \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha ) = 0\).
(iii) Find \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha )\) and hence show that the value of \(\alpha \) never exceeds 10°.
Find the set of values of \(x\) for which \(\alpha \geqslant 7^\circ \).
Answer/Explanation
Markscheme
EITHER
\(\alpha = \arctan \frac{7}{{10}} – \arctan \frac{5}{{10}}{\text{ }}( = 34.992 \ldots ^\circ – 26.5651 \ldots ^\circ )\) (M1)(A1)(A1)
Note: Award (M1) for \(\alpha = {\rm{A\hat PT}} – {\rm{B\hat PT}}\), (A1) for a correct \({\rm{A\hat PT}}\) and (A1) for a correct \({\rm{B\hat PT}}\).
OR
\(\alpha = \arctan {\text{ }}2 – \arctan \frac{{10}}{7}{\text{ }}( = 63.434 \ldots ^\circ – 55.008 \ldots ^\circ )\) (M1)(A1)(A1)
Note: Award (M1) for \(\alpha = {\rm{P\hat BT}} – {\rm{P\hat AT}}\), (A1) for a correct \({\rm{P\hat BT}}\) and (A1) for a correct \({\rm{P\hat AT}}\).
OR
\(\alpha = \arccos \left( {\frac{{125 + 149 – 4}}{{2 \times \sqrt {125} \times \sqrt {149} }}} \right)\) (M1)(A1)(A1)
Note: Award (M1) for use of cosine rule, (A1) for a correct numerator and (A1) for a correct denominator.
THEN
\( = 8.43^\circ \) A1
[4 marks]
EITHER
\(\tan \alpha = \frac{{\frac{7}{x} – \frac{5}{x}}}{{1 + \left( {\frac{7}{x}} \right)\left( {\frac{5}{x}} \right)}}\) M1A1A1
Note: Award M1 for use of \(\tan (A – B)\), A1 for a correct numerator and A1 for a correct denominator.
\( = \frac{{\frac{2}{x}}}{{1 + \frac{{35}}{{{x^2}}}}}\) M1
OR
\(\tan \alpha = \frac{{\frac{x}{5} – \frac{x}{7}}}{{1 + \left( {\frac{x}{5}} \right)\left( {\frac{x}{7}} \right)}}\) M1A1A1
Note: Award M1 for use of xxx, A1 for a correct numerator and A1 for a correct denominator.
\( = \frac{{\frac{{2x}}{{35}}}}{{1 + \frac{{{x^2}}}{{35}}}}\) M1
OR
\(\cos \alpha = \frac{{{x^2} + 35}}{{\sqrt {({x^2} + 25)({x^2} + 49)} }}\) M1A1
Note: Award M1 for either use of the cosine rule or use of \(\cos (A – B)\).
\(\sin \alpha \frac{{2x}}{{\sqrt {({x^2} + 25)({x^2} + 49)} }}\) A1
\(\tan \alpha = \frac{{\frac{{2x}}{{\sqrt {({x^2} + 25)({x^2} + 49)} }}}}{{\frac{{{x^2} + 35}}{{\sqrt {({x^2} + 25)({x^2} + 49)} }}}}\) M1
THEN
\(\tan \alpha = \frac{{2x}}{{{x^2} + 35}}\) AG
[4 marks]
(i) \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha ) = \frac{{2({x^2} + 35) – (2x)(2x)}}{{{{({x^2} + 35)}^2}}}{\text{ }}\left( { = \frac{{70 – 2{x^2}}}{{{{({x^2} + 35)}^2}}}} \right)\) M1A1A1
Note: Award M1 for attempting product or quotient rule differentiation, A1 for a correct numerator and A1 for a correct denominator.
(ii) METHOD 1
EITHER
\(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha ) = 0 \Rightarrow 70 – 2{x^2} = 0\) (M1)
\(x = \sqrt {35} {\text{ (m) }}\left( { = 5.9161 \ldots {\text{ (m)}}} \right)\) A1
\(\tan \alpha = \frac{1}{{\sqrt {35} }}{\text{ }}( = 0.16903 \ldots )\) (A1)
OR
attempting to locate the stationary point on the graph of
\(\tan \alpha = \frac{{2x}}{{{x^2} + 35}}\) (M1)
\(x = 5.9161 \ldots {\text{ (m) }}\left( { = \sqrt {35} {\text{ (m)}}} \right)\) A1
\(\tan \alpha = 0.16903 \ldots {\text{ }}\left( { = \frac{1}{{\sqrt {35} }}} \right)\) (A1)
THEN
\(\alpha = 9.59^\circ \) A1
METHOD 2
EITHER
\(\alpha = \arctan \left( {\frac{{2x}}{{{x^2} + 35}}} \right) \Rightarrow \frac{{{\text{d}}\alpha }}{{{\text{d}}x}} = \frac{{70 – 2{x^2}}}{{{{({x^2} + 35)}^2} + 4{x^2}}}\) M1
\(\frac{{{\text{d}}\alpha }}{{{\text{d}}x}} = 0 \Rightarrow x = \sqrt {35} {\text{ (m) }}\left( { = 5.9161{\text{ (m)}}} \right)\) A1
OR
attempting to locate the stationary point on the graph of
\(\alpha = \arctan \left( {\frac{{2x}}{{{x^2} + 35}}} \right)\) (M1)
\(x = 5.9161 \ldots {\text{ (m) }}\left( { = \sqrt {35} {\text{ (m)}}} \right)\) A1
THEN
\(\alpha = 0.1674 \ldots {\text{ }}\left( { = \arctan \frac{1}{{\sqrt {35} }}} \right)\) (A1)
\( = 9.59^\circ \) A1
(iii) \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha ) = \frac{{{{({x^2} + 25)}^2}( – 4x) – (2)(2x)({x^2} + 35)(70 – 2{x^2})}}{{{{({x^2} + 35)}^4}}}{\text{ }}\left( { = \frac{{4x({x^2} – 105)}}{{{{({x^2} + 35)}^3}}}} \right)\) M1A1
substituting \(x = \sqrt {35} {\text{ }}( = 5.9161 \ldots )\) into \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha )\) M1
\(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha ) < 0{\text{ }}( =- 0.004829 \ldots )\) and so \(\alpha = 9.59^\circ \) is the maximum value of \(\alpha \) R1
\(\alpha \) never exceeds 10° AG
[11 marks]
attempting to solve \(\frac{{2x}}{{{x^2} + 35}} \geqslant \tan 7^\circ \) (M1)
Note: Award (M1) for attempting to solve \(\frac{{2x}}{{{x^2} + 35}} = \tan 7^\circ \).
\(x = 2.55\) and \(x = 13.7\) (A1)
\(2.55 \leqslant x \leqslant 13.7{\text{ (m)}}\) A1
[3 marks]
Examiners report
This question was generally accessible to a large majority of candidates. It was pleasing to see a number of different (and quite clever) trigonometric methods successfully employed to answer part (a) and part (b).
This question was generally accessible to a large majority of candidates. It was pleasing to see a number of different (and quite clever) trigonometric methods successfully employed to answer part (a) and part (b).
The early parts of part (c) were generally well done. In part (c) (i), a few candidates correctly found \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha )\) in unsimplified form but then committed an algebraic error when endeavouring to simplify further. A few candidates merely stated that \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha ) = {\sec ^2}\alpha \).
Part (c) (ii) was reasonably well done with a large number of candidates understanding what was required to find the correct value of \(\alpha \) in degrees. In part (c)(iii), a reasonable number of candidates were able to successfully find \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha )\) in unsimplified form. Some however attempted to solve \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha ) = 0\) for \(\chi \) rather than examine the value of \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha )\) at \(x = \sqrt {35} \).
Part (d), which required use of a GCD to determine an inequality, was surprisingly often omitted by candidates. Of the candidates who attempted this part, a number stated that \(x \geqslant 2.55\). Quite a sizeable proportion of candidates who obtained the correct inequality did not express their answer to 3 significant figures.
