Question
The binary operation \( * \) is defined on the set S = {0, 1, 2, 3} by
\[a * b = a + 2b + ab(\bmod 4){\text{ .}}\]
(a) (i) Construct the Cayley table.
(ii) Write down, with a reason, whether or not your table is a Latin square.
(b) (i) Write down, with a reason, whether or not \( * \) is commutative.
(ii) Determine whether or not \( * \) is associative, justifying your answer.
(c) Find all solutions to the equation \(x * 1 = 2 * x\) , for \(x \in S\) .
▶️Answer/Explanation
Markscheme
(a) (i)
 A3
A3
Note: Award A3 for no errors, A2 for one error, A1 for two errors and A0 for three or more errors.
(ii) it is not a Latin square because some rows/columns contain the same digit more than once A1
[4 marks]
(b) (i) EITHER
it is not commutative because the table is not symmetric about the leading diagonal R2
OR
it is not commutative because \(a + 2b + ab \ne 2a + b + ab\) in general R2
Note: Accept a counter example e.g. \(1 * 2 = 3\) whereas \(2 * 1 = 2\) .
(ii) EITHER
for example \((0 * 1) * 1 = 2 * 1 = 2\) M1
and \(0 * (1 * 1) = 0 * 0 = 0\) A1
so \( * \) is not associative A1
OR
associative if and only if \(a * (b * c) = (a * b) * c\) M1
which gives
\(a + 2b + 4c + 2bc + ab + 2ac + abc = a + 2b + ab + 2c + ac + 2bc + abc\) A1
so \( * \) is not associative as \(2ac \ne 2c + ac\) , in general A1
[5 marks]
(c) x = 0 is a solution A2
x = 2 is a solution A2
[4 marks]
Total [13 marks]
Examiners report
This question was generally well answered.
Question
The binary operation \( * \) is defined on \(\mathbb{N}\) by \(a * b = 1 + ab\).
Determine whether or not \( * \)
a.is closed;[2]
b.is commutative;[2]
c.is associative;[3]
d.has an identity element.[3]
▶️Answer/Explanation
Markscheme
\( * \) is closed A1
because \(1 + ab \in \mathbb{N}\) (when \(a,b \in \mathbb{N}\)) R1
[2 marks]
consider
\(a * b = 1 + ab = 1 + ba = b * a\) M1A1
therefore \( * \) is commutative
[2 marks]
EITHER
\(a * (b * c) = a * (1 + bc) = 1 + a(1 + bc){\text{ }}( = 1 + a + abc)\) A1
\((a * b) * c = (1 + ab) * c = 1 + c(1 + ab){\text{ }}( = 1 + c + abc)\) A1
(these two expressions are unequal when \(a \ne c\)) so \( * \) is not associative R1
OR
proof by counter example, for example
\(1 * (2 * 3) = 1 * 7 = 8\) A1
\((1 * 2) * 3 = 3 * 3 = 10\) A1
(these two numbers are unequal) so \( * \) is not associative R1
[3 marks]
let e denote the identity element; so that
\(a * e = 1 + ae = a\) gives \(e = \frac{{a – 1}}{a}\) (where \(a \ne 0\)) M1
then any valid statement such as: \(\frac{{a – 1}}{a} \notin \mathbb{N}\) or e is not unique R1
there is therefore no identity element A1
Note: Award the final A1 only if the previous R1 is awarded.
[3 marks]
Examiners report
For the commutative property some candidates began by setting \(a * b = b * a\) . For the identity element some candidates confused \(e * a\) and \(ea\) stating \(ea = a\) . Others found an expression for an inverse element but then neglected to state that it did not belong to the set of natural numbers or that it was not unique.
For the commutative property some candidates began by setting \(a * b = b * a\) . For the identity element some candidates confused \(e * a\) and \(ea\) stating \(ea = a\) . Others found an expression for an inverse element but then neglected to state that it did not belong to the set of natural numbers or that it was not unique.
For the commutative property some candidates began by setting \(a * b = b * a\) . For the identity element some candidates confused \(e * a\) and \(ea\) stating \(ea = a\) . Others found an expression for an inverse element but then neglected to state that it did not belong to the set of natural numbers or that it was not unique.
For the commutative property some candidates began by setting \(a * b = b * a\) . For the identity element some candidates confused \(e * a\) and \(ea\) stating \(ea = a\) . Others found an expression for an inverse element but then neglected to state that it did not belong to the set of natural numbers or that it was not unique.
Question
The binary operation \(\Delta\) is defined on the set \(S =\) {1, 2, 3, 4, 5} by the following Cayley table.
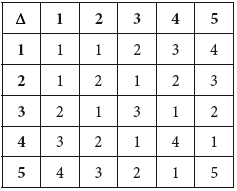
(a) State whether S is closed under the operation Δ and justify your answer.
(b) State whether Δ is commutative and justify your answer.
(c) State whether there is an identity element and justify your answer.
(d) Determine whether Δ is associative and justify your answer.
(e) Find the solutions of the equation \(a\Delta b = 4\Delta b\), for \(a \ne 4\).
▶️Answer/Explanation
Markscheme
(a) yes A1
because the Cayley table only contains elements of S R1
[2 marks]
(b) yes A1
because the Cayley table is symmetric R1
[2 marks]
(c) no A1
because there is no row (and column) with 1, 2, 3, 4, 5 R1
[2 marks]
(d) attempt to calculate \((a\Delta b)\Delta c\) and \(a\Delta (b\Delta c)\) for some \(a,{\text{ }}b,{\text{ }}c \in S\) M1
counterexample: for example, \((1\Delta 2)\Delta 3 = 2\)
\(1\Delta (2\Delta 3) = 1\) A1
Δ is not associative A1
Note: Accept a correct evaluation of \((a\Delta b)\Delta c\) and \(a\Delta (b\Delta c)\) for some \(a,{\text{ }}b,{\text{ }}c \in S\) for the M1.
[3 marks]
(e) for example, attempt to enumerate \(4\Delta b\) for b = 1, 2, 3, 4, 5 and obtain (3, 2, 1, 4, 1) (M1)
find \((a,{\text{ }}b) \in \left\{ {{\text{(2, 2), (2, 3)}}} \right\}\) for \(a \ne 4\) (or equivalent) A1A1
Note: Award M1A1A0 if extra ‘solutions’ are listed.
[3 marks]
Total [12 marks]
Examiners report
Question
The binary operations \( \odot \) and \( * \) are defined on \({\mathbb{R}^ + }\) by
\[a \odot b = \sqrt {ab} {\text{ and }}a * b = {a^2}{b^2}.\]
Determine whether or not
a.\( \odot \) is commutative;[2]
b.\( * \) is associative;[4]
d.\( \odot \) has an identity element.[3]
▶️Answer/Explanation
Markscheme
\(a \odot b = \sqrt {ab} = \sqrt {ba} = b \odot a\) A1
since \(a \odot b = b \odot a\) it follows that \( \odot \) is commutative R1
[2 marks]
\(a * (b * c) = a * {b^2}{c^2} = {a^2}{b^4}{c^4}\) M1A1
\((a * b) * c = {a^2}{b^2} * c = {a^4}{b^4}{c^2}\) A1
these are different, therefore \( * \) is not associative R1
Note: Accept numerical counter-example.
[4 marks]
\(a * (b \odot c) = a * \sqrt {bc} = {a^2}bc\) M1A1
\((a * b) \odot (a * c) = {a^2}{b^2} \odot {a^2}{c^2} = {a^2}bc\) A1
these are equal so \( * \) is distributive over \( \odot \) R1
[4 marks]
the identity e would have to satisfy
\(a \odot e = a\) for all a M1
now \(a \odot e = \sqrt {ae} = a \Rightarrow e = a\) A1
therefore there is no identity element A1
[3 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
