Question
Consider the differential equation \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{{y^2} + {x^2}}}{{2{x^2}}}\) for which y = −1 when x = 1.
(a) Use Euler’s method with a step length of 0.25 to find an estimate for the value of y when x = 2 .
(b) (i) Solve the differential equation giving your answer in the form \(y = f(x)\) .
(ii) Find the value of y when x = 2 .
Answer/Explanation
Markscheme
(a) Using an increment of 0.25 in the x-values A1
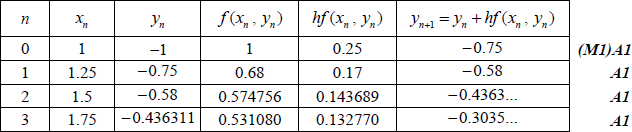
Note: The A1 marks are awarded for final column.
\( \Rightarrow y(2) \approx – 0.304\) A1
[7 marks]
(b) (i) let y = vx M1
\( \Rightarrow \frac{{{\text{d}}y}}{{{\text{d}}x}} = v + x\frac{{{\text{d}}v}}{{{\text{d}}x}}\) (A1)
\( \Rightarrow v + x\frac{{{\text{d}}v}}{{{\text{d}}x}} = \frac{{{v^2}{x^2} + {x^2}}}{{2{x^2}}}\) (M1)
\( \Rightarrow x\frac{{{\text{d}}v}}{{{\text{d}}x}} = \frac{{1 – 2v + {v^2}}}{2}\) (A1)
\( \Rightarrow x\frac{{{\text{d}}v}}{{{\text{d}}x}} = \frac{{{{(1 – v)}^2}}}{2}\) A1
\( \Rightarrow \int {\frac{2}{{{{(1 – v)}^2}}}{\text{d}}v = \int {\frac{1}{x}{\text{d}}x} } \) M1
\( \Rightarrow 2{(1 – v)^{ – 1}} = \ln x + c\) A1A1
\( \Rightarrow \frac{2}{{1 – \frac{y}{x}}} = \ln x + c\)
when \(x = 1,{\text{ }}y = – 1 \Rightarrow c = 1\) M1A1
\( \Rightarrow \frac{{2x}}{{x – y}} = \ln x + 1\)
\( \Rightarrow y = x – \frac{{2x}}{{1 + \ln x}}{\text{ }}\left( { = \frac{{x\ln x – x}}{{1 + \ln x}}} \right)\) M1A1
(ii) when \(x = 2,{\text{ }}y = – 0.362\,\,\,\,\,\left( {{\text{accept 2}} – \frac{4}{{1 + \ln 2}}} \right)\) A1
[13 marks]
Total [20 marks]
Examiners report
Part (a) was well done by many candidates, but a number were penalised for not using a sufficient number of significant figures. Part (b) was started by the majority of candidates, but only the better candidates were able to reach the end. Many were unable to complete the question correctly because they did not know what to do with the substitution y = vx and because of arithmetic errors and algebraic errors.
Question
Solve the differential equation
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{y}{x} + \frac{{{y^2}}}{{{x^2}}}\) (where x > 0 )
given that y = 2 when x = 1 . Give your answer in the form \(y = f(x)\) .
Answer/Explanation
Markscheme
put y = vx so that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = v + x\frac{{{\text{d}}v}}{{{\text{d}}x}}\) M1A1
the equation becomes \(v + x\frac{{{\text{d}}v}}{{{\text{d}}x}} = v + {v^2}\) (A1)
leading to \(x\frac{{{\text{d}}v}}{{{\text{d}}x}} = {v^2}\) A1
separating variables, \(\int {\frac{{{\text{d}}x}}{x} = \int {\frac{{{\text{d}}v}}{{{v^2}}}} } \) M1A1
hence \(\ln x = – {v^{ – 1}} + C\) A1A1
substituting for v, \(\ln x = \frac{{ – x}}{y} + C\) M1
Note: Do not penalise absence of C at the above stages.
substituting the boundary conditions,
\(0 = – \frac{1}{2} + C\) M1
\(C = \frac{1}{2}\) A1
the solution is \(\ln x = \frac{{ – x}}{y} + \frac{1}{2}\) (A1)
leading to \(y = \frac{{2x}}{{1 – 2\ln x}}\) (or equivalent form) A1
Note: Candidates are not required to note that \(x \ne \sqrt {\text{e}} \) .
[13 marks]
Examiners report
Many candidates were able to make a reasonable attempt at this question with many perfect solutions seen.
Question
Solve the differential equation
\[{x^2}\frac{{{\text{d}}y}}{{{\text{d}}x}} = {y^2} + xy + 4{x^2},\]
given that y = 2 when x =1. Give your answer in the form \(y = f(x)\).
Answer/Explanation
Markscheme
put \(y = vx\) so that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = v + x\frac{{{\text{d}}v}}{{{\text{d}}x}}\) (M1)
the equation becomes \(v + x\frac{{{\text{d}}v}}{{{\text{d}}x}} = {v^2} + v + 4\) A1
\(\int {\frac{{{\text{d}}v}}{{{v^2} + 4}} = \int {\frac{{{\text{d}}x}}{x}} } \) A1
\(\frac{1}{2}\arctan \left( {\frac{v}{2}} \right) = \ln x + C\) A1A1
substituting\((x,{\text{ }}v) = (1,{\text{ }}2)\)
\(C = \frac{\pi }{8}\) M1A1
the solution is
\(\arctan \left( {\frac{y}{{2x}}} \right) = 2\ln x + \frac{\pi }{4}\) A1
\(y = 2x\tan \left( {2\ln x + \frac{\pi }{4}} \right)\) A1
[9 marks]
Examiners report
Most candidates recognised this differential equation as one in which the substitution \(y = vx\) would be helpful and many carried the method through to a successful conclusion. The most common error seen was an incorrect integration of \(\frac{1}{{4 + {v^2}}}\) with partial fractions and/or a logarithmic evaluation seen. Some candidates failed to include an arbitrary constant which led to a loss of marks later on.
Question
Solve the differential equation
\({x^2}\frac{{{\text{d}}y}}{{{\text{d}}x}} = {y^2} + 3xy + 2{x^2}\)
given that y = −1 when x =1. Give your answer in the form \(y = f(x)\) .
Answer/Explanation
Markscheme
put y = vx so that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = v + x\frac{{{\text{d}}v}}{{{\text{d}}x}}\) M1
substituting, M1
\(v + x\frac{{{\text{d}}v}}{{{\text{d}}x}} = \frac{{{v^2}{x^2} + 3v{x^2} + 2{x^2}}}{{{x^2}}}{\text{ }}( = {v^2} + 3v + 2)\) (A1)
\(x\frac{{{\text{d}}v}}{{{\text{d}}x}} = {v^2} + 2v + 2\) A1
\(\int {\frac{{{\text{d}}v}}{{{v^2} + 2v + 2}} = \int {\frac{{{\text{d}}x}}{x}} } \) M1
\(\int {\frac{{{\text{d}}v}}{{{{(v + 1)}^2} + 1}} = \int {\frac{{{\text{d}}x}}{x}} } \) (A1)
\(\arctan (v + 1) = \ln x + c\) A1
Note: Condone absence of c at this stage.
\(\arctan (\frac{y}{x} + 1) = \ln x + c\) M1
When x = 1, y = −1 M1
c = 0 A1
\(\frac{y}{x} + 1 = \tan \ln x\)
\(y = x(\tan \ln x – 1)\) A1
[11 marks]
Examiners report
Most candidates recognised this differential equation as one in which the substitution y = vx would be helpful and many reached the stage of separating the variables. However, the integration of \(\frac{1}{{{v^2} + 2v + 2}}\) proved beyond many candidates who failed to realise that completing the square would lead to an arctan integral. This highlights the importance of students having a full understanding of the core calculus if they are studying this option.
Question
Find the general solution of the differential equation \(t\frac{{{\text{d}}y}}{{{\text{d}}t}} = \cos t – 2y\) , for t > 0 .
Answer/Explanation
Markscheme
recognise equation as first order linear and attempt to find the IF M1
\({\text{IF}} = {{\text{e}}^{\int {\frac{2}{t}{\text{d}}t} }} = {t^2}\) A1
solution \(y{t^2} = \int {t\cos t{\text{d}}t} \) M1A1
using integration by parts with the correct choice of u and v (M1)
\(\int {t\cos t{\text{d}}t = t\sin t + \cos t( + C)} \) A1
obtain \(y = \frac{{\sin t}}{t} + \frac{{\cos t + C}}{{{t^2}}}\) A1
[7 marks]
Examiners report
Perhaps a small number of candidates were put off by the unusual choice of variables but in most instances it seemed that candidates who recognised the need for an integration factor could make a good attempt at this problem. Candidates who were not able to simplify the integrating factor from \({e^{2\ln t}}\) to \({t^2}\) rarely gained full marks. A significant number of candidates did not gain the final mark due to a lack of an arbitrary constant or not dividing the constant by the integration factor.
Question
Consider the differential equation \(x\frac{{{\text{d}}y}}{{{\text{d}}x}} – y = {x^p} + 1\) where \(x \in \mathbb{R},\,x \ne 0\) and \(p\) is a positive integer, \(p > 1\).
Solve the differential equation given that \(y = – 1\) when \(x = 1\). Give your answer in the form \(y = f\left( x \right)\).
Show that the \(x\)-coordinate(s) of the points on the curve \(y = f\left( x \right)\) where \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) satisfy the equation \({x^{p – 1}} = \frac{1}{p}\).
Deduce the set of values for \(p\) such that there are two points on the curve \(y = f\left( x \right)\) where \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\). Give a reason for your answer.
Answer/Explanation
Markscheme
METHOD 1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{y}{x} = {x^{p – 1}} + \frac{1}{x}\) (M1)
integrating factor \( = {{\text{e}}^{\int { – \frac{1}{x}{\text{d}}x} }}\) M1
\({\text{ = }}{{\text{e}}^{ – {\text{ln}}\,x}}\) (A1)
= \(\frac{1}{x}\) A1
\(\frac{1}{x}\frac{{{\text{d}}y}}{{{\text{d}}x}} – \frac{y}{{{x^2}}} = {x^{p – 2}} + \frac{1}{{{x^2}}}\) (M1)
\(\frac{{\text{d}}}{{{\text{d}}x}}\left( {\frac{y}{x}} \right) = {x^{p – 2}} + \frac{1}{{{x^2}}}\)
\(\frac{y}{x} = \frac{1}{{p – 1}}{x^{p – 1}} – \frac{1}{x} + C\) A1
Note: Condone the absence of C.
\(y = \frac{1}{{p – 1}}{x^p} + Cx – 1\)
substituting \(x = 1\), \(y = – 1 \Rightarrow C = – \frac{1}{{p – 1}}\) M1
Note: Award M1 for attempting to find their value of C.
\(y = \frac{1}{{p – 1}}\left( {{x^p} – x} \right) – 1\) A1
[8 marks]
METHOD 2
put \(y = vx\) so that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = v + x\frac{{{\text{d}}v}}{{{\text{d}}x}}\) M1(A1)
substituting, M1
\(x\left( {v + x\frac{{{\text{d}}v}}{{{\text{d}}x}}} \right) – vx = {x^p} + 1\) (A1)
\(x\frac{{{\text{d}}v}}{{{\text{d}}x}} = {x^{p – 1}} + \frac{1}{x}\) M1
\(\frac{{{\text{d}}v}}{{{\text{d}}x}} = {x^{p – 2}} + \frac{1}{{{x^2}}}\)
\(v = \frac{1}{{p – 1}}{x^{p – 1}} – \frac{1}{x} + C\) A1
Note: Condone the absence of C.
\(y = \frac{1}{{p – 1}}{x^p} + Cx – 1\)
substituting \(x = 1\), \(y = – 1 \Rightarrow C = – \frac{1}{{p – 1}}\) M1
Note: Award M1 for attempting to find their value of C.
\(y = \frac{1}{{p – 1}}\left( {{x^p} – x} \right) – 1\) A1
[8 marks]
METHOD 1
find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) and solve \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) for \(x\)
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{1}{{p – 1}}\left( {p{x^{p – 1}} – 1} \right)\) M1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0 \Rightarrow p{x^{p – 1}} – 1 = 0\) A1
\(p{x^{p – 1}} = 1\)
Note: Award a maximum of M1A0 if a candidate’s answer to part (a) is incorrect.
\({x^{p – 1}} = \frac{1}{p}\) AG
METHOD 2
substitute \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) and their \(y\) into the differential equation and solve for \(x\)
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0 \Rightarrow – \left( {\frac{{{x^p} – x}}{{p – 1}}} \right) + 1 = {x^p} + 1\) M1
\({x^p} – x = {x^p} – p{x^p}\) A1
\(p{x^{p – 1}} = 1\)
Note: Award a maximum of M1A0 if a candidate’s answer to part (a) is incorrect.
\({x^{p – 1}} = \frac{1}{p}\) AG
[2 marks]
there are two solutions for \(x\) when \(p\) is odd (and \(p > 1\) A1
if \(p – 1\) is even there are two solutions (to \({x^{p – 1}} = \frac{1}{p}\))
and if \(p – 1\) is odd there is only one solution (to \({x^{p – 1}} = \frac{1}{p}\)) R1
Note: Only award the R1 if both cases are considered.
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]

