Question
The mean value theorem states that if \(f\) is a continuous function on \([a,{\text{ }}b]\) and differentiable on \(]a,{\text{ }}b[\) then \(f'(c) = \frac{{f(b) – f(a)}}{{b – a}}\) for some \(c \in ]a,{\text{ }}b[\).
(i) Find the two possible values of \(c\) for the function defined by \(f(x) = {x^3} + 3{x^2} – 2\) on the interval \([ – 3,{\text{ }}1]\).
(ii) Illustrate this result graphically.[7]
(i) The function \(f\) is continuous on \([a,{\text{ }}b]\), differentiable on \(]a,{\text{ }}b[\) and \(f'(x) = 0\) for all \(x \in ]a,{\text{ }}b[\). Show that \(f(x)\) is constant on \([a,{\text{ }}b]\).
(ii) Hence, prove that for \(x \in [0,{\text{ }}1],{\text{ }}2\arccos x + \arccos (1 – 2{x^2}) = \pi \).[9]
▶️Answer/Explanation
Markscheme
(i) \(f'(x) = 3{x^2} + 6x\) A1
gradient of chord \( = 1\) A1
\(3{c^2} + 6c = 1\)
\(c = \frac{{ – 3 \pm 2\sqrt 3 }}{3}{\text{ }}( = – 2.15,{\text{ }}0.155)\) A1A1
Note: Accept any answers that round to the correct 2sf answers \(( – 2.2,{\text{ }}0.15)\).
(ii) 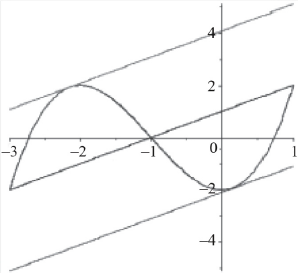
award A1 for correct shape and clear indication of correct domain, A1 for chord (from \(x = – 3\) to \(x = 1\)) and A1 for two tangents drawn at their values of \(c\) A1A1A1
[7 marks]
(i) METHOD 1
(if a theorem is true for the interval \([a,{\text{ }}b]\), it is also true for any interval \([{x_1},{\text{ }}{x_2}]\) which belongs to \([a,{\text{ }}b]\))
suppose \({x_1},{\text{ }}{x_2} \in [a,{\text{ }}b]\) M1
by the \(MVT\), there exists \(c\) such that \(f'(c) = \frac{{f({x_2}) – f({x_1})}}{{{x_2} – {x_1}}} = 0\) M1A1
hence \(f({x_1}) = f({x_2})\) R1
as \({x_1},{\text{ }}{x_2}\) are arbitrarily chosen, \(f(x)\) is constant on \([a,{\text{ }}b]\)
Note: If the above is expressed in terms of \(a\) and \(b\) award M0M1A0R0.
METHOD 2
(if a theorem is true for the interval \([a,{\text{ }}b]\), it is also true for any interval \([{x_1},{\text{ }}{x_2}]\) which belongs to \([a,{\text{ }}b]\))
suppose \(x \in [a,{\text{ }}b]\) M1
by the \(MVT\), there exists \(c\) such that \(f'(c) = \frac{{f(x) – f(a)}}{{x – a}} = 0\) M1A1
hence \(f(x) = f(a) = \) constant R1
(ii) attempt to differentiate \((x) = 2\arccos x + \arccos (1 – 2{x^2})\) M1
\( – 2\frac{1}{{\sqrt {1 – {x^2}} }} – \frac{{ – 4x}}{{\sqrt {1 – {{(1 – 2{x^2})}^2}} }}\) A1A1
\( = – 2\frac{1}{{\sqrt {1 – {x^2}} }} + \frac{{4x}}{{\sqrt {4{x^2} – 4{x^4}} }} = 0\) A1
Note: Only award A1 for \(0\) if a correct attempt to simplify the denominator is also seen.
\(f(x) = f(0) = 2 \times \frac{\pi }{2} + 0 = \pi \) A1AG
Note: This A1 is not dependent on previous marks.
Note: Allow any value of \(x \in [0,{\text{ }}1]\).
[9 marks]
Total [16 marks]
Examiners report
(i) This was well done by most candidates.
(ii) This was generally poorly done, with many candidates failing to draw the curve correctly as they did not appreciate the importance of the given domain. Another common error was to draw the graph of the derivative rather than the function.
(i) This was very poorly done. A lot of the arguments seemed to be stating what was being required to be proved, eg ‘because the derivative is equal to 0 the line is flat’. Most candidates did not realise the importance of testing a point inside the interval, so the most common solutions seen involved the Mean Value Theorem applied to the end points. In addition there was some confusion between the Mean Value Theorem and Rolle’s Theorem.
(ii) It was pleasing that so many candidates spotted the link with the previous part of the question. The most common error after this point was to differentiate incorrectly. Candidates should be aware this is a ‘prove’ question, and so it was not sufficient simply to state, for example, \(f(0) = \pi \).
Question
The function \(f\) is defined by \(f(x) = {{\text{e}}^x}\sin x,{\text{ }}x \in \mathbb{R}\).
The Maclaurin series is to be used to find an approximate value for \(f(0.5)\).
a.By finding a suitable number of derivatives of \(f\), determine the Maclaurin series for \(f(x)\) as far as the term in \({x^3}\).[7]
b.Hence, or otherwise, determine the exact value of \(\mathop {\lim }\limits_{x \to 0} \frac{{{{\text{e}}^x}\sin x – x – {x^2}}}{{{x^3}}}\).[3]
c.(i) Use the Lagrange form of the error term to find an upper bound for the absolute value of the error in this approximation.
(ii) Deduce from the Lagrange error term whether the approximation will be greater than or less than the actual value of \(f(0.5)\).[7]
▶️Answer/Explanation
Markscheme
attempt to use product rule (M1)
\(f'(x) = {{\text{e}}^x}\sin x + {{\text{e}}^x}\cos x\) A1
\(f”(x) = 2{{\text{e}}^x}\cos x\) A1
\(f”(x) = 2{{\text{e}}^x}\cos x – 2{{\text{e}}^x}\sin x\) A1
\(f(0) = 0,{\text{ }}f'(0) = 1\)
\(f”(0) = 2,{\text{ }}f”'(0) = 2\) (M1)
\({{\text{e}}^x}\sin x = x + {x^2} + \frac{{{x^3}}}{3} + \ldots \) (M1)A1
[7 marks]
METHOD 1
\(\frac{{{{\text{e}}^x}\sin x – x – {x^2}}}{{{x^3}}} = \frac{{x + {x^2} + \frac{{{x^3}}}{3} + \ldots – x – {x^2}}}{{{x^3}}}\) M1A1
\( \to \frac{1}{3}\) as \(x \to 0\) A1
METHOD 2
\(\mathop {\lim }\limits_{x \to 0} \frac{{{{\text{e}}^x}\sin x – x – {x^2}}}{{{x^3}}} = \mathop {\lim }\limits_{x \to 0} \frac{{{{\text{e}}^x}\sin x + {{\text{e}}^x}\cos x – 1 – 2x}}{{3{x^2}}}\) A1
\( = \mathop {\lim }\limits_{x \to 0} \frac{{2{{\text{e}}^x}\cos x – 2}}{{6x}}\) A1
\( = \mathop {\lim }\limits_{x \to 0} \frac{{2{{\text{e}}^x}\cos x – 2{{\text{e}}^x}\sin x}}{6} = \frac{1}{3}\) A1
[3 marks]
(i) attempt to find \({{\text{4}}^{{\text{th}}}}\) derivative from the \({{\text{3}}^{{\text{rd}}}}\) derivative obtained in (a) M1
\(f””(x) = – 4{{\text{e}}^x}\sin x\) A1
Lagrange error term \( = \frac{{{f^{(n + 1)}}(c){x^{n + 1}}}}{{(n + 1)!}}\) (where c lies between 0 and \(x\))
\( = – \frac{{4{{\text{e}}^c}\sin c \times {{0.5}^4}}}{{4!}}\) (M1)
the maximum absolute value of this expression occurs when \(c = 0.5\) (A1)
Note: This A1 is independent of previous M marks.
therefore
upper bound \( = \frac{{4{{\text{e}}^{0.5}}\sin 0.5 \times {{0.5}^4}}}{{4!}}\) (M1)
\( = 0.00823\) A1
(ii) the approximation is greater than the actual value because the Lagrange error term is negative R1
[7 marks]
Examiners report
This part of the question was well answered by most candidates. In a few cases candidates failed to follow instructions and attempted to use known series; in a few cases mistakes in the determination of the derivatives prevented other candidates from achieving full marks; part (b) was also well answered using both the Maclaurin expansion or L’Hôpital rule; again in most cases that candidates failed to achieve full marks were due to mistakes in the determination of derivatives.
Part (a) of the question was well answered by most candidates. In a few cases candidates failed to follow instructions and attempted to use known series; in a few cases mistakes in the determination of the derivatives prevented other candidates from achieving full marks; part (b) was also well answered using both the Maclaurin expansion or L’Hôpital rule; again in most cases that candidates failed to achieve full marks were due to mistakes in the determination of derivatives.
Part (c) was poorly answered with few candidates showing familiarity with this part of the option. Most candidates quoted the formula and managed to find the \({4^{{\text{th}}}}\) derivative of \(f\) but then could not use it to obtain the required answer; in other cases candidates did obtain an answer but showed little understanding of its meaning when answering (c)(ii).
Question
a.By successive differentiation find the first four non-zero terms in the Maclaurin series for \(f(x) = (x + 1)\ln (1 + x) – x\).[11]
b.Deduce that, for \(n \geqslant 2\), the coefficient of \({x^n}\) in this series is \({( – 1)^n}\frac{1}{{n(n – 1)}}\).[1]
c.By applying the ratio test, find the radius of convergence for this Maclaurin series.[6]
▶️Answer/Explanation
Markscheme
\(f(x) = (x + 1)\ln (1 + x) – x\) \(f(0) = 0\) A1
\(f'(x) = \ln (1 + x) + \frac{{x + 1}}{{1 + x}} – 1{\text{ }}\left( { = \ln (1 + x)} \right)\) \(f'(0) = 0\) M1A1A1
\(f”(x) = {(1 + x)^{ – 1}}\) \(f”(0) = 1\) A1A1
\(f”'(x) = – {(1 + x)^{ – 2}}\) \(f”'(0) = – 1\) A1
\({f^{(4)}}(x) = 2{(1 + x)^{ – 3}}\) \({f^{(4)}}(0) = 2\) A1
\({f^{(5)}}(x) = – 3 \times 2{(1 + x)^{ – 4}}\) \({f^{(5)}}(0) = – 3 \times 2\) A1
\(f(x) = \frac{{{x^2}}}{{2!}} – \frac{{1{x^3}}}{{3!}} + \frac{{2{x^4}}}{{4!}} – \frac{{6{x^5}}}{{5!}} \ldots \) M1A1
\(f(x) = \frac{{{x^2}}}{{1 \times 2}} – \frac{{{x^3}}}{{2 \times 3}} + \frac{{{x^4}}}{{3 \times 4}} – \frac{{{x^5}}}{{4 \times 5}} \ldots \)
\(f(x) = \frac{{{x^2}}}{2} – \frac{{{x^3}}}{6} + \frac{{{x^4}}}{{12}} – \frac{{{x^5}}}{{20}} \ldots \)
Note: Allow follow through from the first error in a derivative (provided future derivatives also include the chain rule), no follow through after a second error in a derivative.
[11 marks]
\({f^{(n)}}(0) = {( – 1)^n}(n – 2)!\) So coefficient of \({x^n} = {( – 1)^n}\frac{{(n – 2)!}}{{n!}}\) A1
coefficient of \({x^n}\) is \({( – 1)^n}\frac{1}{{n(n – 1)}}\) AG
[1 mark]
applying the ratio test to the series of absolute terms
\(\mathop {\lim }\limits_{n \to \infty } \frac{{\frac{{{{\left| x \right|}^{n + 1}}}}{{(n + 1)n}}}}{{\frac{{{{\left| x \right|}^n}}}{{n(n – 1)}}}}\) M1A1
\( = \mathop {\lim }\limits_{n \to \infty } \left| x \right|\frac{{(n – 1)}}{{(n + 1)}}\) A1
\( = \left| x \right|\) A1
so for convergence \(\left| x \right| < 1\), giving radius of convergence as 1 (M1)A1
[6 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
Let \(f(x)\) be a function whose first and second derivatives both exist on the closed interval \([0,{\text{ }}h]\).
Let \(g(x) = f(h) – f(x) – (h – x)f'(x) – \frac{{{{(h – x)}^2}}}{{{h^2}}}\left( {f(h) – f(0) – hf'(0)} \right)\).
a.State the mean value theorem for a function that is continuous on the closed interval \([a,{\text{ }}b]\) and differentiable on the open interval \(]a,{\text{ }}b[\).[2]
b.(i) Find \(g(0)\).
(ii) Find \(g(h)\).
(iii) Apply the mean value theorem to the function \(g(x)\) on the closed interval \([0,{\text{ }}h]\) to show that there exists \(c\) in the open interval \(]0,{\text{ }}h[\) such that \(g'(c) = 0\).
(iv) Find \(g'(x)\).
(v) Hence show that \( – (h – c)f”(c) + \frac{{2(h – c)}}{{{h^2}}}\left( {f(h) – f(0) – hf'(0)} \right) = 0\).
(vi) Deduce that \(f(h) = f(0) + hf'(0) + \frac{{{h^2}}}{2}{\text{ }}f”(c)\).[9]
c.Hence show that, for \(h > 0\)
\(1 – \cos (h) \leqslant \frac{{{h^2}}}{2}\).[5]
▶️Answer/Explanation
Markscheme
there exists \(c\) in the open interval \(]a,{\text{ }}b[\) such that A1
\(\frac{{f(b) – f(a)}}{{b – a}} = f'(c)\) A1
Note: Open interval is required for the A1.
[2 marks]
(i) \(g(0) = f(h) – f(0) – hf'(0) – \frac{{{h^2}}}{{{h^2}}}\left( {{\text{ }}f(h) – f(0) – hf'(0)} \right)\)
\( = 0\) A1
(ii) \(g(h) = f(h) – f(h) – 0 – 0\)
\( = 0\) A1
(iii) (\(g(x)\) is a differentiable function since it is a combination of other differentiable functions \(f\), \({f’}\) and polynomials.)
there exists \(c\) in the open interval \(]0,{\text{ }}h[\) such that
\(\frac{{g(h) – g(0)}}{h} = g'(c)\) A1
\(\frac{{g(h) – g(0)}}{h} = 0\) A1
hence \(g'(c) = 0\) AG
(iv) \(g'(x) = – f'(x) + f'(x) – (h – x)f”(x) + \frac{{2(h – x)}}{{{h^2}}}\left( {f(h) – f(0) – hf'(0)} \right)\) A1A1
Note: A1 for the second and third terms and A1 for the other terms (all terms must be seen).
\( = – (h – x)f”(x) + \frac{{2(h – x)}}{{{h^2}}}\left( {f(h) – f(0) – hf'(0)} \right)\)
(v) putting \(x = c\) and equating to zero M1
\( – (h – c)f”(c) + \frac{{2(h – c)}}{{{h^2}}}\left( {f(h) – f(0) – hf'(0)} \right) = g'(c) = 0\) AG
(vi) \( – f”(c) + \frac{2}{{{h^2}}}\left( {f(h) – f(0) – hf'(0)} \right) = 0\) A1
since \(h – c \ne 0\) R1
\(\frac{{{h^2}}}{2}f”(c) = f(h) – f(0) – hf'(0)\)
\(f(h) = f(0) + hf'(0) + \frac{{{h^2}}}{2}f”(c)\) AG
[9 marks]
letting \(f(x) = \cos (x)\) M1
\(f'(x) = – \sin (x)\) \(f”(x) = – \cos (x)\) A1
\(\cos (h) = 1 + 0 – \frac{{{h^2}}}{2}\cos (c)\) A1
\(1 – \cos (h) = \frac{{{h^2}}}{2}\cos (c)\) (A1)
since \(\cos (c) \leqslant 1\) R1
\(1 – \cos (h) \leqslant \frac{{{h^2}}}{2}\) AG
Note: Allow \(f(x) = a \pm b\cos x\).
[5 marks]
Examiners report
[N/A]
[N/A]
[N/A]
