Question
A function is defined as \(f(x) = k\sqrt x \), with \(k > 0\) and \(x \geqslant 0\) .
(a) Sketch the graph of \(y = f(x)\) .
(b) Show that f is a one-to-one function.
(c) Find the inverse function, \({f^{ – 1}}(x)\) and state its domain.
(d) If the graphs of \(y = f(x)\) and \(y = {f^{ – 1}}(x)\) intersect at the point (4, 4) find the value of k .
(e) Consider the graphs of \(y = f(x)\) and \(y = {f^{ – 1}}(x)\) using the value of k found in part (d).
(i) Find the area enclosed by the two graphs.
(ii) The line x = c cuts the graphs of \(y = f(x)\) and \(y = {f^{ – 1}}(x)\) at the points P and Q respectively. Given that the tangent to \(y = f(x)\) at point P is parallel to the tangent to \(y = {f^{ – 1}}(x)\) at point Q find the value of c .
▶️Answer/Explanation
Markscheme
(a)
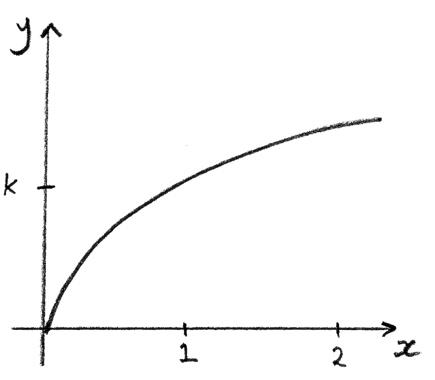A1
Note: Award A1 for correct concavity, passing through (0, 0) and increasing.
Scales need not be there.
[1 mark]
(b) a statement involving the application of the Horizontal Line Test or equivalent A1
[1 mark]
(c) \(y = k\sqrt x \)
for either \(x = k\sqrt y \) or \(x = \frac{{{y^2}}}{{{k^2}}}\) A1
\({f^{ – 1}}(x) = \frac{{{x^2}}}{{{k^2}}}\) A1
\({\text{dom}}\left( {{f^{ – 1}}(x)} \right) = \left[ {0,\infty } \right[\) A1
[3 marks]
(d) \(\frac{{{x^2}}}{{{k^2}}} = k\sqrt x \,\,\,\,\,\)or equivalent method M1
\(k = \sqrt x \)
\(k = 2\) A1
[2 marks]
(e) (i) \(A = \int_a^b {({y_1} – {y_2}){\text{d}}x} \) (M1)
\(A = \int_0^4 {\left( {2{x^{\frac{1}{2}}} – \frac{1}{4}{x^2}} \right){\text{d}}x} \) A1
\( = \left[ {\frac{4}{3}{x^{\frac{3}{2}}} – \frac{1}{{12}}{x^3}} \right]_0^4\) A1
\( = \frac{{16}}{3}\) A1
(ii) attempt to find either \(f'(x)\) or \(({f^{ – 1}})'(x)\) M1
\(f'(x) = \frac{1}{{\sqrt x }},{\text{ }}\left( {({f^{ – 1}})'(x) = \frac{x}{2}} \right)\) A1A1
\(\frac{1}{{\sqrt c }} = \frac{c}{2}\) M1
\(c = {2^{\frac{2}{3}}}\) A1
[9 marks]
Total [16 marks]
Question
The graph of \(y = \frac{{a + x}}{{b + cx}}\) is drawn below.
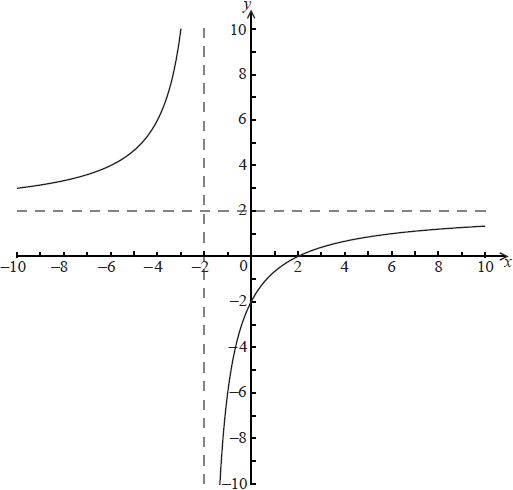
(a) Find the value of a, the value of b and the value of c.
(b) Using the values of a, b and c found in part (a), sketch the graph of \(y = \left| {\frac{{b + cx}}{{a + x}}} \right|\) on the axes below, showing clearly all intercepts and asymptotes.
▶️Answer/Explanation
Markscheme
(a) an attempt to use either asymptotes or intercepts (M1)
\(a = – 2,{\text{ }}b = 1,{\text{ }}c = \frac{1}{2}\) A1A1A1
(b)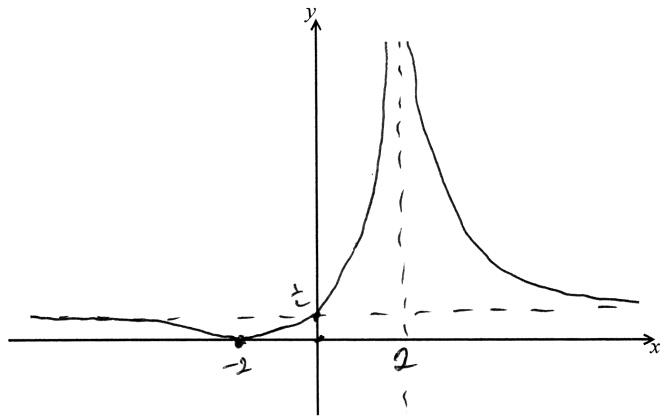 
A4
Note: Award A1 for both asymptotes,
A1 for both intercepts,
A1, A1 for the shape of each branch, ignoring shape at \((x = – 2)\).
[8 marks]
Question
The diagram below shows the graph of the function \(y = f(x)\) , defined for all \(x \in \mathbb{R}\),
where \(b > a > 0\) .
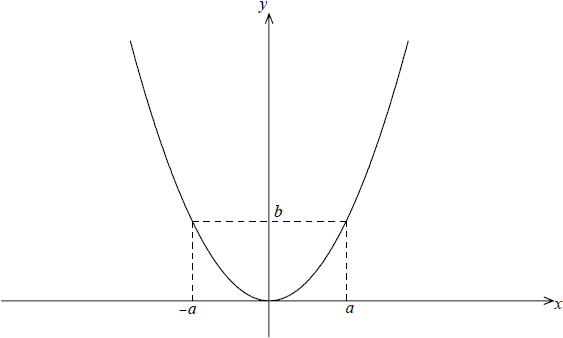
Consider the function \(g(x) = \frac{1}{{f(x – a) – b}}\).
a.Find the largest possible domain of the function \(g\) .[2]
b.On the axes below, sketch the graph of \(y = g(x)\) . On the graph, indicate any asymptotes and local maxima or minima, and write down their equations and coordinates.
[6]
▶️Answer/Explanation
Markscheme
\(f(x – a) \ne b\) (M1)
\(x \ne 0\) and \(x \ne 2a\) (or equivalent) A1
[2 marks]
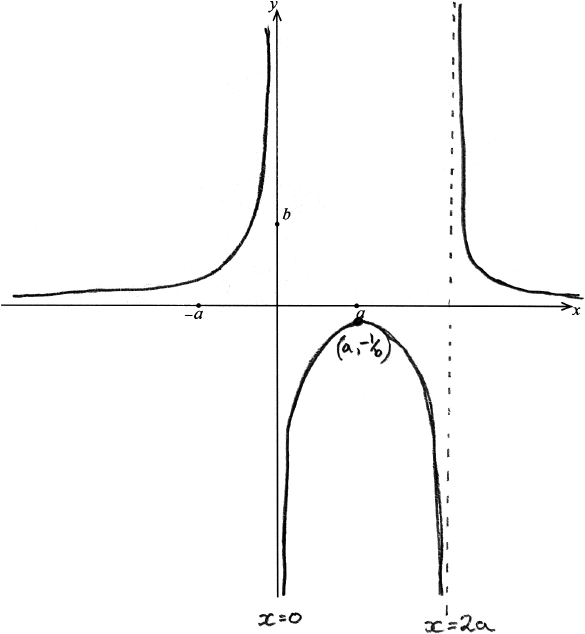
vertical asymptotes \(x = 0\), \(x = 2a\) A1
horizontal asymptote \(y = 0\) A1
Note: Equations must be seen to award these marks.
maximum \(\left( {a, – \frac{1}{b}} \right)\) A1A1
Note: Award A1 for correct x-coordinate and A1 for correct y-coordinate.
one branch correct shape A1
other 2 branches correct shape A1
[6 marks]
Question
Consider the function \(f(x) = \frac{{\ln x}}{x}\) , \(0 < x < {{\text{e}}^2}\) .
a.(i) Solve the equation \(f'(x) = 0\) .
(ii) Hence show the graph of \(f\) has a local maximum.
(iii) Write down the range of the function \(f\) .[5]
b.Show that there is a point of inflexion on the graph and determine its coordinates.[5]
c.Sketch the graph of \(y = f(x)\) , indicating clearly the asymptote, x-intercept and the local maximum.[3]
d.Now consider the functions \(g(x) = \frac{{\ln \left| x \right|}}{x}\) and \(h(x) = \frac{{\ln \left| x \right|}}{{\left| x \right|}}\) , where \(0 < x < {{\text{e}}^2}\) .
(i) Sketch the graph of \(y = g(x)\) .
(ii) Write down the range of \(g\) .
(iii) Find the values of \(x\) such that \(h(x) > g(x)\) .[6]
▶️Answer/Explanation
Markscheme
(i) \(f'(x) = \frac{{x\frac{1}{x} – \ln x}}{{{x^2}}}\) M1A1
\( = \frac{{1 – \ln x}}{{{x^2}}}\)
so \(f'(x) = 0\) when \(\ln x = 1\), i.e. \(x = {\text{e}}\) A1
(ii) \(f'(x) > 0\) when \(x < {\text{e}}\) and \(f'(x) < 0\) when \(x > {\text{e}}\) R1
hence local maximum AG
Note: Accept argument using correct second derivative.
(iii) \(y \leqslant \frac{1}{{\text{e}}}\) A1
[5 marks]
\(f”(x) = \frac{{{x^2}\frac{{ – 1}}{x} – \left( {1 – \ln x} \right)2x}}{{{x^4}}}\) M1
\( = \frac{{ – x – 2x + 2x\ln x}}{{{x^4}}}\)
\( = \frac{{ – 3 + 2\ln x}}{{{x^3}}}\) A1
Note: May be seen in part (a).
\(f”(x) = 0\) (M1)
\({ – 3 + 2\ln x = 0}\)
\(x = {{\text{e}}^{\frac{3}{2}}}\)
since \(f”(x) < 0\) when \(x < {{\text{e}}^{\frac{3}{2}}}\) and \(f”(x) > 0\) when \(x > {{\text{e}}^{\frac{3}{2}}}\) R1
then point of inflexion \(\left( {{{\text{e}}^{\frac{3}{2}}},\frac{3}{{2{{\text{e}}^{\frac{3}{2}}}}}} \right)\) A1
[5 marks]
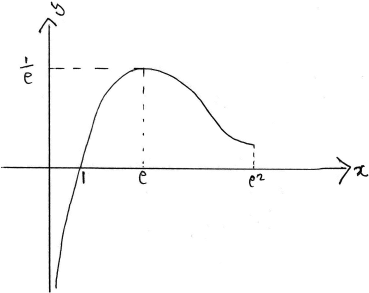A1A1A1
Note: Award A1 for the maximum and intercept, A1 for a vertical asymptote and A1 for shape (including turning concave up).
[3 marks]
(i)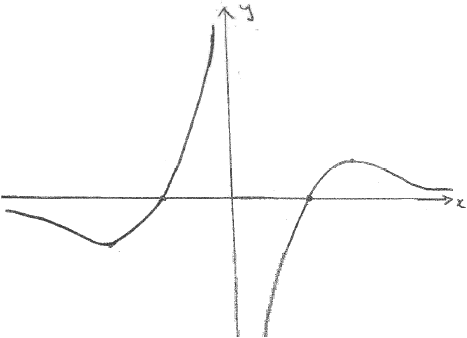
A1A1
Note: Award A1 for each correct branch.
(ii) all real values A1
(iii)
(M1)(A1)
Note: Award (M1)(A1) for sketching the graph of h, ignoring any graph of g.
\( – {{\text{e}}^2} < x < – 1\) (accept \(x < – 1\) ) A1
[6 marks]
Question
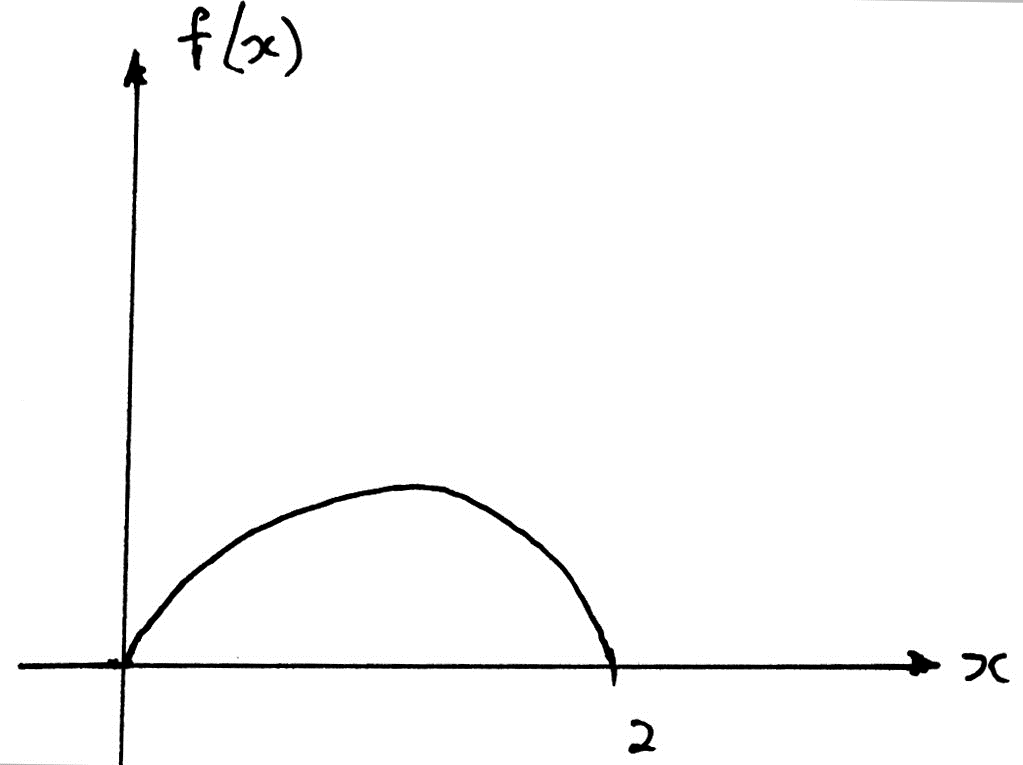
The random variable X has probability density function f where
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{kx(x + 1)(2 – x),}&{0 \leqslant x \leqslant 2} \\
{0,}&{{\text{otherwise }}{\text{.}}}
\end{array}} \right.\]
a.Sketch the graph of the function. You are not required to find the coordinates of the maximum.[1]
b.Find the value of k .[5]
▶️Answer/Explanation
Markscheme
A1
Note: Award A1 for intercepts of 0 and 2 and a concave down curve in the given domain .
Note: Award A0 if the cubic graph is extended outside the domain [0, 2] .
[1 mark]
\(\int_0^2 {kx(x + 1)(2 – x){\text{d}}x = 1} \) (M1)
Note: The correct limits and =1 must be seen but may be seen later.
\(k\int_0^2 {( – {x^3} + {x^2} + 2x){\text{d}}x = 1} \) A1
\(k\left[ { – \frac{1}{4}{x^4} + \frac{1}{3}{x^3} + {x^2}} \right]_0^2 = 1\) M1
\(k\left( { – 4 + \frac{8}{3} + 4} \right) = 1\) (A1)
\(k = \frac{3}{8}\) A1
[5 marks]